1. Линейность:  .
.
2. Подобие: 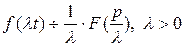 .
.
3. Смещение:  .
.
4. Запаздывание: 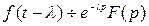 ,
,  >0.
>0.
5. Дифференцирование оригинала:

………………………………………………
 .
.
6. Дифференцирование изображения:

…………………………
 .
.
7. Интегрирование оригинала:  .
.
8. Интегрирование изображения:  .
.
9. Умножение изображений (теорема о свертке функций):
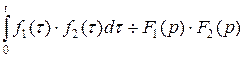 .
.
Приведем краткую таблицу, устанавливающую соответствие между некоторыми оригиналами (часто встречающимися на практике) и их изображениями.
Таблица оригиналов и изображений Таблица 2
| № | Оригинал f(t) | Изображение  | № | Оригинал f(t) | Изображение  |
 |  |  | |||
 |  |  |  | ||
| t |  | 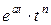 |  | ||
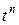 (n - целое) (n - целое) |  |  |  | ||
 |  |  |  | ||
 |  |  |  | ||
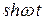 | 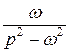 |  | 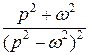 | ||
 |  |  | 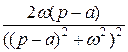 | ||
 |  |  | 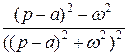 | ||
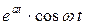 |  |  |  |
Достаточно полная таблица оригиналов и изображений, позволяющая по заданному оригиналу находить изображение и наоборот, есть, в частности, в книге «Справочник по операционному исчислению» (авторы В.А. Диткин и П.И. Кузнецов).
Õ Пример. Используя таблицу изображений и свойства, найти изображения оригиналов:
1) 
Найдем изображение каждого слагаемого, используя в таблице формулы 1, 4 и 15

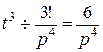

Используя свойство линейности, получаем:

2) 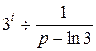 (формула 20).
(формула 20).
3)  (формула 5).
(формула 5).
4) 
Используем формулу  . Далее, используем свойство линейности и формулу 5, получаем:
. Далее, используем свойство линейности и формулу 5, получаем:
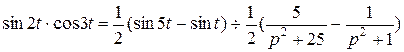 .
.
5)  (формулы 1 и 6).
(формулы 1 и 6).
6)  . Используем свойство 6 (дифференцирование изображения):
. Используем свойство 6 (дифференцирование изображения):
если f(t) ÷ F(p), то 

Получили  .
.
7)  . Изображение гиперболического косинуса известно
. Изображение гиперболического косинуса известно 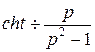 , применяя свойство смещения
, применяя свойство смещения  , получаем
, получаем 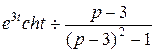 .
.
8)  . Используем теорему об интегрировании оригинала (свойство 7):
. Используем теорему об интегрировании оригинала (свойство 7):
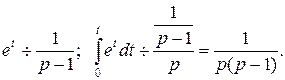
9)  (свойство 7). n
(свойство 7). n
Õ Пример. Найти оригиналы по изображениям.
На практике рекомендуется поступать следующим образом:
- по таблице оригиналов и изображений попытаться отыскать для заданного изображения F(p) соответствующий ему оригинал.
- функцию  представить в виде суммы простейших рациональных дробей, а затем, пользуясь свойством линейности и таблицей найти оригинал.
представить в виде суммы простейших рациональных дробей, а затем, пользуясь свойством линейности и таблицей найти оригинал.
1) 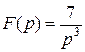
По таблице (формула 4)  . Умножим и разделим исходное изображение на 2:
. Умножим и разделим исходное изображение на 2: 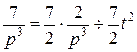 . Искомый оригинал
. Искомый оригинал  .
.
2) 
Выделим полный квадрат в знаменателе и применим формулу 9:
 .
.
Получили оригинал 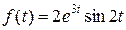 .
.
3) 
Для нахождения оригинала используем формулу 13 и свойство линейности:

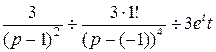 .
.
Искомый оригинал 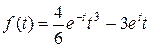 .
.
4)  . Выделим в знаменателе полный квадрат и применим формулы 9 и 10, свойство линейности:
. Выделим в знаменателе полный квадрат и применим формулы 9 и 10, свойство линейности:

5) 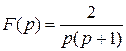
Представим дробь в виде суммы простейших дробей:
 .
.
Приравниваем числители дробей и находим коэффициенты А и В:


Далее используем свойство линейности и формулы 1, 2:

Искомый оригинал  .n
.n
 2015-10-22
2015-10-22 6369
6369
