Уравнение прямой по точке и направляющему вектору

Направляющим вектором прямой l называется всякий ненулевой вектор 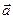(m, n), параллельный этой прямой.

Пусть заданы точка M ₁(x ₁, y ₁) и направляющий вектор 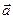(m, n), тогда уравнение прямой, проходящей через точку M ₁ в направлении вектора 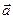имеет вид: 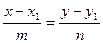. Это уравнение называется каноническим уравнением прямой.

Пример. Найти уравнение прямой с направляющим вектором 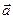(1, -1) и проходящей через точку А(1, 2).

Уравнение искомой прямой будем искать в виде: Ax + By + C = 0. Запишем каноническое уравнение прямой 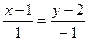, преобразуем его. Получим х + у - 3 = 0