Практическое занятие №12

Наименование занятия: Вычисление производных сложных функций

Цель занятия: Научиться находить производные.

Подготовка к занятию: Повторить теоретический материал по теме «Дифференциальное исчисление функции одной действительной переменной»

Литература:

1. Григорьев В.П., Дубинский Ю.А. «Элементы высшей математики», 2008г.
2. Дадаян А.А. «Математика», 2004г.

Задание на занятие:

1. Найти производные следующих функций:

1) ;

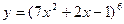2) ;

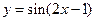3) ;

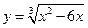4) ;

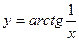5)

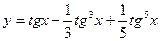
6) ;

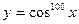7) ;

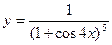8) ;

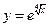9) ;

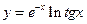10) .

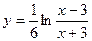2. Вычислить производные функций в заданных точках:

1) 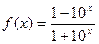Найти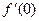

2) 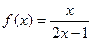Найти , ,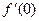

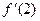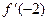
3) 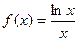Найти , ,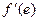

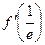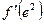
Порядок проведения занятия:

1. Получить допуск к работе
2. Выполнить задания
3. Ответить на контрольные вопросы.

Содержание отчета:

1. Наименование, цель занятия, задание;
2. Выполненное задание;
3. Ответы на контрольные вопросы.

Контрольные вопросы для зачета:

1. Что называется производной функции?
2. Как найти производную от сложной функции?
3. Как вычислить частное значение производной?

ПРИЛОЖЕНИЕ

Рассмотрим функцию у = f (x) при х принадлежащему некоторому отрезку [ a; b ]. Возьмем произвольную точку х₀ из этого отрезка.

Производной функции f(x) в точке х₀ называется предел отношения приращения функции Δf (x₀) к приращению аргумента Δх при Δх → 0 (если этот предел существует).

Таким образом, = =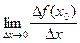

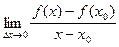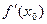
Если этот предел конечный, то функция называется дифференцируемой в точке x_o.