Наименование занятия: Нахождение производных высших порядков. Правила Лопиталя.
Цель занятия: Научиться находить производные высших порядков, применять правило Лопиталя к вычислению пределов.
Подготовка к занятию: Повторить теоретический материал по теме «Дифференциальное исчисление функции одной действительной переменной»
Литература:
- Григорьев В.П., Дубинский Ю.А. «Элементы высшей математики», 2008г.
Задание на занятие:
1. Найти производные 2-го следующих функций.
1) 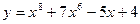 ;
;
2) 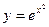 ;
;
3) 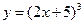 ;
;
4) 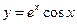 ;
;
5) 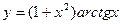 .
.
2. Дана функция 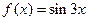 . Найти
. Найти 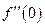 ,
, 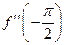 ,
, 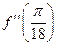 .
.
3. Вычислить производные 3-го порядка следующих функций.
1) 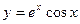 ;
;
2) 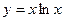
4. Дана функция 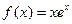 . Найти
. Найти 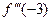 ,
, 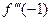 ,
, 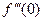 .
.
3. Вычислить пределы, используя правило Лопиталя.
1) 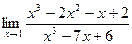 ;
;
2) 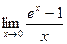 ;
;
3) 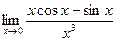 ;
;
4) 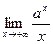 ;
;
5) 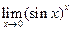 .
.
Порядок проведения занятия:
- Получить допуск к работе
- Выполнить задания
- Ответить на контрольные вопросы.
Содержание отчета:
- Наименование, цель занятия, задание;
- Выполненное задание;
- Ответы на контрольные вопросы.
Контрольные вопросы для зачета:
- Что называется производной второго порядка? п -го порядка?
- Сформулируйте правило Лопиталя.
ПРИЛОЖЕНИЕ
Производные высших порядков
Пусть функция f(x)- дифференцируема на некотором интервале. Тогда, дифференцируя ее, получаем первую производную 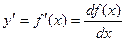
Если найти производную функции f¢(x), получим вторую производную функции f(x):
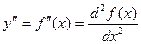 , т.е. y¢¢ = (y¢)¢ или
, т.е. y¢¢ = (y¢)¢ или 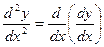 .
.
Этот процесс можно продолжить и далее, находя производные степени n: 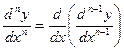 .
.
 2015-06-24
2015-06-24 649
649








