Теорема Лопиталя. Если функции f(x) и g(x) дифференцируемы в окрестности точки а, непрерывны в точке а, g¢(x) отлична от нуля в окрестности точки а и f(a) = g(a) = 0, то предел отношения функций при х®а равен пределу отношения их производных, если этот предел (конечный или бесконечный) существует.
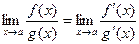
Замечание. Теорема остается в силе и в том случае, когда в точке x = a функции j (x) и y (x) обращаются в бесконечность.
Правило Лопиталя. Для раскрытия неопределенностей 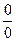 и
и 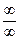 надо заменить предел отношения двух функций пределом отношения их производных. Если окажется, что отношение производных имеет конечный предел, то к этому же пределу стремится и отношение данных функций.
надо заменить предел отношения двух функций пределом отношения их производных. Если окажется, что отношение производных имеет конечный предел, то к этому же пределу стремится и отношение данных функций.
Пример: Найти предел 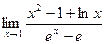 .
.
При попытке непосредственного вычисления предела получается неопределенность вида 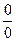 . Функции, входящие в числитель и знаменатель дроби удовлетворяют требованиям теоремы Лопиталя: f¢(x) = 2 x +
. Функции, входящие в числитель и знаменатель дроби удовлетворяют требованиям теоремы Лопиталя: f¢(x) = 2 x + 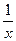 ; g¢(x) = ex. Тогда
; g¢(x) = ex. Тогда 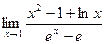 =
= 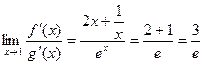 .
.
Если при решении примера после применения правила Лопиталя попытка вычислить предел опять приводит к неопределенности, то правило Лопиталя может быть применено второй раз, третий и т.д. пока не будет получен результат. Естественно, это возможно только в том случае, если вновь полученные функции в свою очередь удовлетворяют требованиям теоремы Лопиталя.
Пример: Найти предел 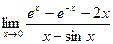 .
.
При подстановке х = 0 получается неопределенность вида 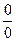 . Применим правило Лопиталя. Найдем производные числителя и знаменателя:
. Применим правило Лопиталя. Найдем производные числителя и знаменателя: 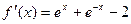 ;
; 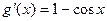 и подставим их в предел:
и подставим их в предел: 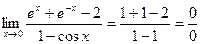 - опять получилась неопределенность. Применим правило Лопиталя еще раз.
- опять получилась неопределенность. Применим правило Лопиталя еще раз. 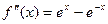 ;
; 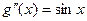 ;
;
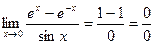 - применяем правило Лопиталя еще раз.
- применяем правило Лопиталя еще раз.
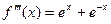 ;
; 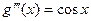 ;
; 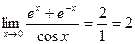 .
.
Для раскрытия других неопределенностей 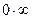 ,
, 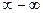 ,
, 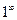 ,
, 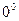 их следует предварительно преобразовать к неопределенности вида
их следует предварительно преобразовать к неопределенности вида 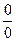 или
или 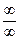 .
.
Пример 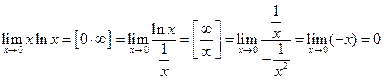
Неопределенности вида 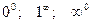 можно раскрыть с помощью логарифмирования. Такие неопределенности встречаются при нахождении пределов функций вида
можно раскрыть с помощью логарифмирования. Такие неопределенности встречаются при нахождении пределов функций вида 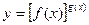 , f(x)> 0 в окрестности точки а при х® а. Для нахождения предела такой функции достаточно найти предел функции ln y = g(x) ln f(x).
, f(x)> 0 в окрестности точки а при х® а. Для нахождения предела такой функции достаточно найти предел функции ln y = g(x) ln f(x).
Пример: Найти предел 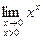 .
.
Здесь y = xx, ln y = x ln x.
Тогда 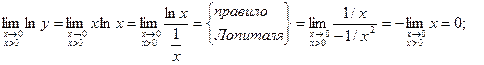 .
.
Следовательно 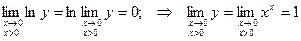
 2015-06-24
2015-06-24 8733
8733
