Рассмотрим метод Жуковского построения вектора 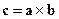 .
.
Пусть угол между векторами  и
и  равен
равен 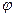 .
.
Векторы  и
и  приложим к общему началу
приложим к общему началу 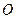 (рис. 2.20).
(рис. 2.20).
Через точку 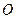 перпендикулярно вектору
перпендикулярно вектору  проведем плоскость
проведем плоскость 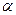 . Из конца вектора
. Из конца вектора  опустим перпендикуляр на плоскость
опустим перпендикуляр на плоскость 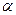 .
.
Точку пересечения этого перпендикуляра и плоскости обозначим через 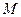 . Проведем в плоскости
. Проведем в плоскости 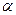 вектор
вектор 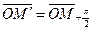 и построим вектор
и построим вектор 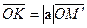 .
.
Рис. 2.20 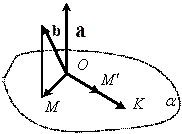 Покажем, что вектор
Покажем, что вектор 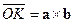 .
.
а) Из построения следует, что вектор 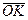 перпендикулярен
перпендикулярен
векторам  ,
,  , и векторы
, и векторы  ,
,  ,
, 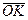 образуют правую тройку.
образуют правую тройку.
б) 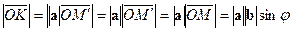 .
.
Из а) и б) следует, что 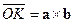 .
.
Если проекцию вектора  на плоскость
на плоскость 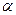 обозначить через
обозначить через 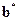
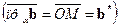 , то
, то
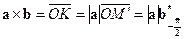 .
.
 2015-06-24
2015-06-24 606
606








