Скалярное произведение векторов применяется для нахождения длины вектора, косинуса угла между векторами, проекции одного вектора на направление другого и установления перпендикулярности векторов.
1) 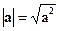 или
или 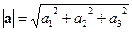 .
.
2) 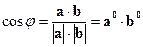 .
.
3) 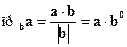 .
.
4) 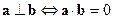 .
.
● Пример 9. Дано: 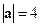 ,
, 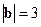 ,
, 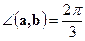 ,
, 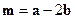 ,
, 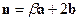 .
.
Найти: а) длину вектора 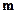 ;
;
б) значение параметра 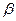 , при котором векторы
, при котором векторы 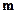 и
и 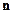 перпендикулярны.
перпендикулярны.
Решение. а) 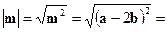
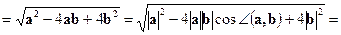
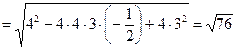 ;
;
б) 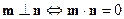 .
.
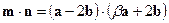
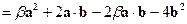 =
=
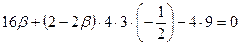 , откуда
, откуда 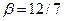 .
.
При 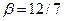 векторы
векторы  и
и 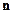 перпендикулярны.
перпендикулярны.
● Пример 10. Даны два вектора 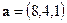 ,
, 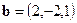 , приложенные к одной точке. Найти вектор
, приложенные к одной точке. Найти вектор 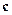 , перпендикулярный вектору
, перпендикулярный вектору  , равный ему по длине, компланарный с векторами
, равный ему по длине, компланарный с векторами  ,
,  и образующий с вектором
и образующий с вектором  острый угол.
острый угол.
Решение. Так как векторы  ,
,  ,
, 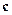 компланарны, а векторы
компланарны, а векторы  и
и  неколлинеарны, то вектор
неколлинеарны, то вектор 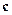 может быть разложен по векторам
может быть разложен по векторам  и
и  . Найдутся такие числа
. Найдутся такие числа 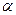 и
и 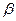 , что
, что 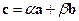 . Тогда
. Тогда 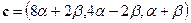 . Вектор
. Вектор 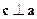 , поэтому скалярное произведение
, поэтому скалярное произведение 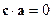 .
. 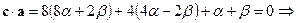
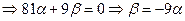 и
и 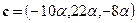 .
.
Вектор 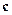 образует с вектором
образует с вектором  острый угол, поэтому косинус угла между этими векторами положителен и
острый угол, поэтому косинус угла между этими векторами положителен и 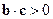 .
.
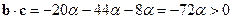 , откуда
, откуда 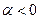 .
.
Так как 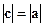 , то
, то 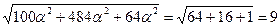 и
и 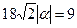 , откуда
, откуда 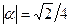 . Учитывая, что
. Учитывая, что 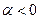 , имеем
, имеем 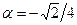 и
и 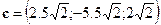 . ●
. ●
 2015-06-24
2015-06-24 6548
6548








