Векторное произведение векторов  и
и  применяется:
применяется:
для нахождения площади параллелограмма, построенного на векторах  и
и  ;
;
для нахождения площади треугольника, построенного на векторах  и
и  ;
;
для нахождения синуса угла между векторами  и
и  ;
;
для нахождения вектора, перпендикулярного векторам  и
и  .
.
1) Площадь 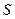 параллелограмма, построенного на векторах
параллелограмма, построенного на векторах  и
и  , может быть вычислена по формуле
, может быть вычислена по формуле 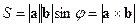 , где
, где 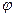 - угол между векторами
- угол между векторами  и
и  .
.
Замечание. Если 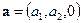 и
и 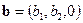 , то
, то 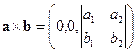 и
и 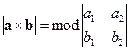 . Отсюда следует, что модуль определителя второго порядка численно равен площади параллелограмма, построенного на векторах
. Отсюда следует, что модуль определителя второго порядка численно равен площади параллелограмма, построенного на векторах 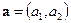 и
и 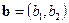 .
.
2) Площадь 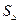 треугольника, построенного на векторах
треугольника, построенного на векторах  и
и  , равна половине площади параллелограмма, построенного на этих же векторах, т.е.
, равна половине площади параллелограмма, построенного на этих же векторах, т.е. 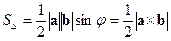 , где
, где 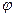 - угол между векторами
- угол между векторами  и
и  .
.
3) Синус угла между векторами  и
и  может быть вычислен по формуле
может быть вычислен по формуле 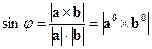 .
.
4) Вектор 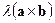 перпендикулярен вектору
перпендикулярен вектору  и вектору
и вектору  .
.
Замечание. Векторное произведение может быть использовано при решении системы линейных однородных уравнений вида 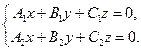 Если векторы
Если векторы 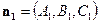 и
и 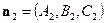 неколлинеарны, то
неколлинеарны, то 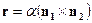 является решением исходной системы.
является решением исходной системы.
►Действительно, из системы уравнений следует, что вектор 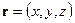 перпендикулярен векторам
перпендикулярен векторам 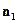 и
и 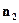 , а, следовательно,
, а, следовательно, 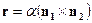 . ◄
. ◄
● Пример 12. Дано: 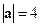 ,
, 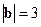 ,
, 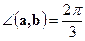 ,
, 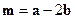 ,
, 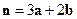 .
.
Найти площадь параллелограмма, построенного на векторах 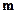 и
и 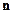 .
.
Найти синус угла 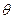 между векторами
между векторами 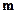 и
и 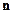 .
.
Решение. Площадь параллелограмма, построенного на векторах 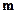 и
и 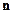 равна модулю векторного произведения векторов
равна модулю векторного произведения векторов 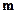 и
и 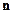 , т.е.
, т.е. 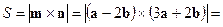
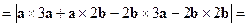
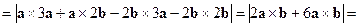
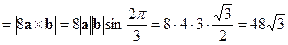 .
.
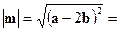
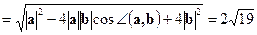 .
.
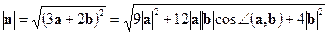 =
= 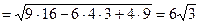 .
.
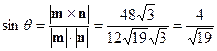 .
.
Ответ: 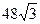 ,
, 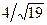 .
.
● Пример 13. Дано: 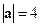 ,
, 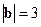 ,
, 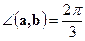 ,
, 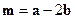 ,
, 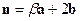 .
.
Найти значение параметра 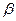 , при котором векторы
, при котором векторы 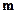 и
и 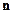 коллинеарны.
коллинеарны.
Решение. Первый способ. Так как векторы 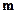 и
и 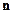 коллинеарны, то их векторное произведение равно нулю.
коллинеарны, то их векторное произведение равно нулю. 
 =0, а так как
=0, а так как 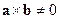 , то
, то 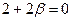 и
и 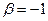 .
.
Второй способ. Векторы  и
и  составляют базис системы векторов
составляют базис системы векторов  ,
,  ,
, 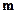 и
и 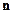 . В базисе
. В базисе 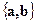
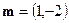 и
и 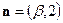 . Так как векторы
. Так как векторы 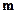 и
и 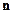 коллинеарны, то
коллинеарны, то 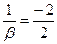 , откуда
, откуда 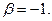 ●
●
● Пример 14. Найти координаты вектора 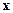 , длина которого равна 15, зная, что он перпендикулярен оси
, длина которого равна 15, зная, что он перпендикулярен оси 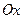 и вектору
и вектору 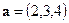 и образует острый угол с осью
и образует острый угол с осью 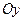 .
.
Решение. 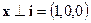 и
и 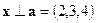 , поэтому
, поэтому 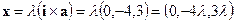 .
.
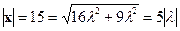 , откуда
, откуда 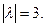
Так как вектор 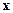 образует острый угол с осью
образует острый угол с осью 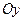 , то вторая его координата положительна, тогда
, то вторая его координата положительна, тогда 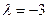 и
и 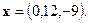 ●
●
● Пример 15. Найти площадь параллелограмма 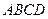 , если известны координаты трёх его вершин
, если известны координаты трёх его вершин 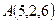 ,
, 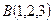 и
и 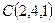 .
.
Решение. 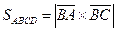 .
. 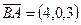 ,
, 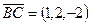 ,
, 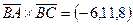 ,
, 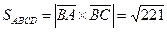 .
.
● Пример 16. 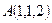 ,
, 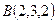 ,
, 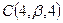 - вершины треугольника
- вершины треугольника 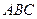 . Найти недостающую координату
. Найти недостающую координату 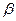 точки
точки 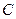 . если площадь треугольника
. если площадь треугольника 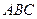 равна 3.
равна 3.
Решение. Площадь 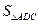 равна половине площади параллелограмма, построенного на векторах
равна половине площади параллелограмма, построенного на векторах 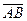 и
и  , т.е.
, т.е. 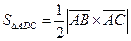 .
.
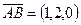 ,
, 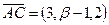 ,
, 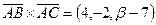 .
. 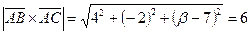 , откуда
, откуда 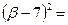 16,
16, 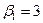 и
и 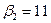 .
.
Ответ: 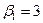 или
или 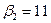 .
.
● Пример 17. Решить систему 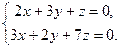
Решение. Из уравнений системы следует, что вектор 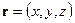 перпендикулярен векторам
перпендикулярен векторам 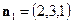 и
и 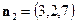 . Тогда
. Тогда 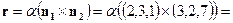
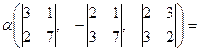
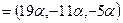 - решение данной системы. ●
- решение данной системы. ●
 2015-06-24
2015-06-24 7554
7554








