Идею предельного перехода проиллюстрируем на следующих примерах.
Пример 17. Решить в классе непрерывных функций уравнение
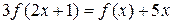 (6.1)
(6.1)
где х 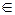 R.
R.
Решение. Заменив х на 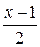 , получим
, получим
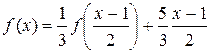 (6.2)
(6.2)
Используя ту же замену, из уравнения (6.2) последовательно получим
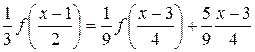 ,
,
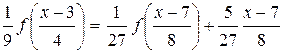 ,
,
……………………………………..
Методом математической индукции можно доказать, что
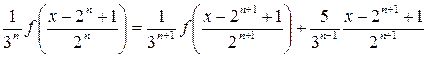 (6.3)
(6.3)
Сложив все уравнения, начиная с (6.2), получим
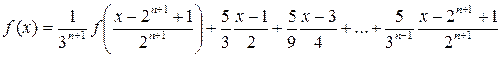 (6.4)
(6.4)
Так как функция f(х) непрерывна, то при любом фиксированном х
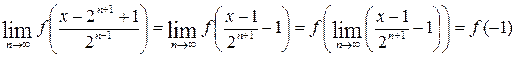
Здесь 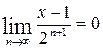 . Из (6.1)
. Из (6.1) 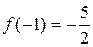 . Тогда
. Тогда
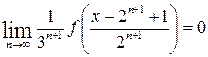
Левая часть равенства (6.4) не зависит от n, поэтому существует ее предел при n → ∞. Переходя к пределу в равенстве (6.4), при n → ∞ имеем
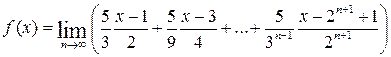 (6.5)
(6.5)
Правая часть (6.5) является суммой трех бесконечно убывающих прогрессий
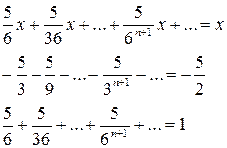
Итак, 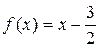 , что и подтверждается проверкой.
, что и подтверждается проверкой.
Пример 18. Функция f: R→R непрерывна в точке 0 и для любого x 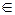 R выполнено равенство
R выполнено равенство
2f(2x) = f(x)+x.
Найти все такие f.
Решение. Пусть функция f удовлетворяет условию. Тогда
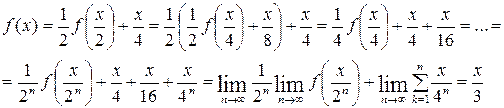
Тривиальная проверка показывает, что функция x/3 действительно является искомой.
Пример 19. Доказать, что уравнение
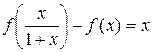 ,
, 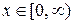 (6.6)
(6.6)
не имеет непрерывных решений.
Решение. Допустим, что существует непрерывное решение функционального уравнения (6.6). Подставим в исходное уравнения вместо x выражение
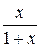
ведь если x ≥ 0, то и
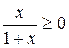
получим:
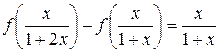 (6.7)
(6.7)
Теперь сделаем такую же замену
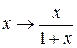
в соотношении (6.7):
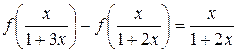 (6.8)
(6.8)
Описанную операцию проделаем ещё несколько pаз. На n-ом шаге имеем:
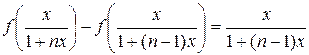
Сложим все получившиеся выражения, начиная с (6.6) (всего будет n выражений), и приведем подобные слагаемые:
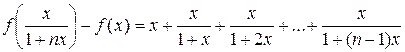 (6.9)
(6.9)
Равенство (6.9) верно для любого натурального n. Зафиксируем x, а n устремим к ∞. Ввиду непрерывности f(x) в точке x = 0, находим
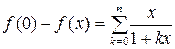 (6.10)
(6.10)
где
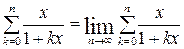
В левой части (6.10) при конкретном (фиксированном) x стоит некоторая константа, т.е. при данном x ряд в правой части (6.10) сходится к этой константе. Мы же покажем, что этот ряд расходится для любого значения x > 0, таким образом, придём к противоречию.
Для любого натурального k и x > 0 верно неравенство
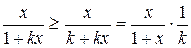
так что
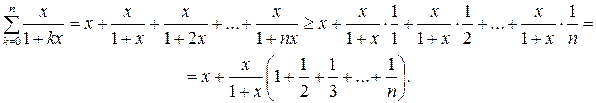
Гармонический ряд
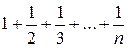
неограниченно возрастает при увеличении n (известный факт), следовательно,
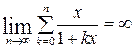
расходится к ∞. Что и требовалось доказать.
Пример 20. Найти f(x), ограниченную на любом конечном интервале, удовлетворяющую функциональному уравнению:
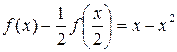
Решение. x = 0 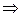 f(0) = 0;
f(0) = 0;
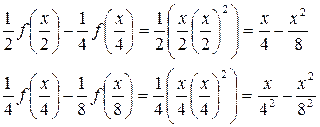
…………………………………………
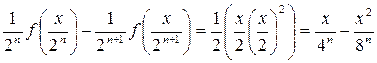
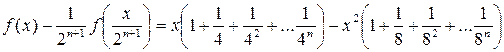
переходя к lim при x → ∞ используя непрерывность f(x) и f(0) = 0 получаем, что
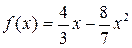 .
.
Пример 21. Решить функциональное уравнение
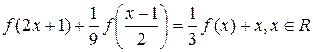 (6.11)
(6.11)
в классе непрерывных функций.
Решение. Выполнив замену 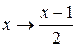 , получим
, получим
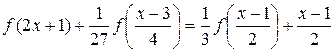 (6.12)
(6.12)
Складывая (6.11) с уравнением (6.12), умноженным на 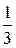 , получим
, получим
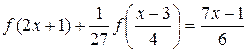
Это уравнение решается аналогично уравнению (6.1). Найдем подстановку, переводящую 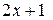 в
в 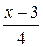 . Для этого положим
. Для этого положим 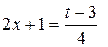 . Отсюда
. Отсюда 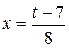 . Выполнив n раз подстановку
. Выполнив n раз подстановку 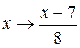 , получим систему уравнений, из которой находим
, получим систему уравнений, из которой находим
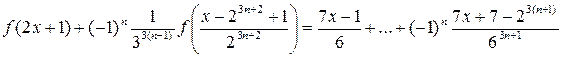
Отсюда при n → ∞
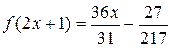 , или
, или 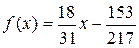 ,
,
что и подтверждается проверкой.
\
 2015-06-24
2015-06-24 679
679








