Признак Коши (радикальный признак)

Если для ряда 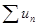с неотрицательными членами существует такое число q<1, что для всех достаточно больших n выполняется неравенство ,

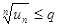то ряд 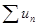сходится, если же для всех достаточно больших n выполняется неравенство 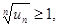то ряд 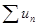расходится.

Теорема. Если существует предел 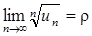, то при r<1 ряд сходится, а при r>1 ряд расходится.

Если l = 1, то на вопрос о сходимости ответить нельзя.

Доказательство аналогично доказательству признака Даламбера.

Пример. Определить сходимость ряда .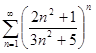

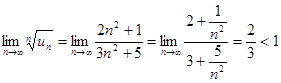Вывод: ряд сходится.

Пример. Определить сходимость ряда .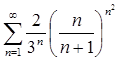

Применим признак к ряду без множителя 2, так как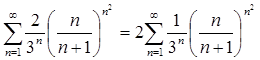

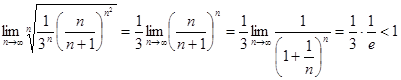- сходится. Тогда по свойству числовых рядов, исходный ряд тоже сходится.

Пример. Определить сходимость ряда .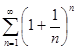

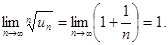- Т.е. признак Коши не дает ответа на вопрос о сходимости ряда. Проверим выполнение необходимых условий сходимости. Как было сказано выше, если ряд сходится, то общий член ряда стремится к нулю.

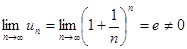, таким образом, необходимое условие сходимости не выполняется, значит, ряд расходится.