Разложение функций в степенной ряд имеет большое значение для решения различных задач исследования функций, дифференцирования, интегрирования, решения дифференциальных уравнений, вычисления пределов, вычисления приближенных значений функции.
Возможны различные способы разложения функции в степенной ряд. Такие способы как разложение при помощи рядов Тейлора и Маклорена были рассмотрены ранее.)
Существует также способ разложения в степенной ряд при помощи алгебраического деления. Это – самый простой способ разложения, однако, пригоден он только для разложения в ряд алгебраических дробей.
Другими способами разложения функции в степенной ряд осуществляется с помощью ряда Тейлора и Маклорена.
Формула Тейлора для функции f(x), определенной в окрестности точки х0 и имеющей в ней производные до (n+1)-го порядка включительно, имеет следующий вид:
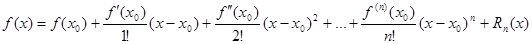 (1),
(1),
где 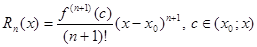 - остаточный член в форме Лагранжа. Число с можно записать в виде
- остаточный член в форме Лагранжа. Число с можно записать в виде 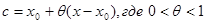 . Формулу кратко можно записать в виде
. Формулу кратко можно записать в виде 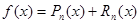 , Pn – многочлен Тейлора.
, Pn – многочлен Тейлора.
Если функция f(x) имеет производные любых порядков в окрестности точки х0 и остаточный член Rn(x) стремится к нулю при 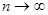 , то из формулы Тейлора получается разложение функции f(x) по степеням (х-х0), называемое рядом Тейлора:
, то из формулы Тейлора получается разложение функции f(x) по степеням (х-х0), называемое рядом Тейлора: 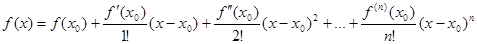 (2).
(2).
Если в ряде Тейлора положить х0=0, то получим разложение функции по степням х в так называемый ряд Маклорена: 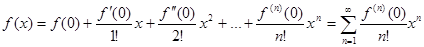 .
.
Теорема. Для того чтобы ряд Тейлора функции f(x) сходился к f(x) в точке х, необходимо и достаточно, чтобы в этой точке остаточный член формулы Тейлора стремился к нулю при 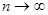 , т.е.
, т.е. 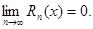
 2015-06-24
2015-06-24 1459
1459
