2015-06-24
2110
Пусть требутся вычислить значение функции f(x) при х=х1 с заданной точностью e>0. Если функцию f(x) в интервале(-R;R) можно разложить в степенной ряд:
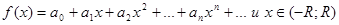, то точное значение f(x1) равно сумме этого ряда при х=х1, т.е. 
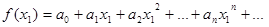, а приближенное – частной сумме 
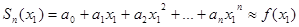. Точность этого равенства увеличивается с ростом n. Абсолютная погрешность этого приближенного равенства равна модулю остатка ряда, т.е. 
.
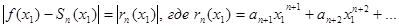Таким, образом, ошибку можно найти оценив остаток ряда.
Для рядов лейбницевского типа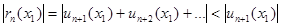 
. В остальных случаях (ряд знакопеременный и знакочередующийся) составляют ряд из модулей членов ряда и для него стараются найти (подобрать) положительный ряд с большеми членами (обычно этосходящийся ряд геометрической прогрессии), который легко бы суммировался. И в качестве оценки берут величину остатка этого нового ряда.
Пример. Найти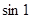 
с точностью до 0,001.
Согласно формуле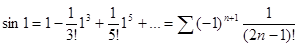 
. Стоящий справа ряд сходится абсолютно. Так как 
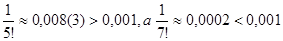, то для нахождения 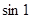с точностью до 0,001 достаточно трех слагаемых: 
.
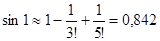Допускаемая ошибка при этом меньше, чем первый отброшенный член.
