Доказательство

Согластно предыдущей теореме, достаточно показать, что 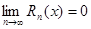. По условию теоремы для любого n имеет место неравенство: 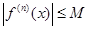. Тогда имеем:

.

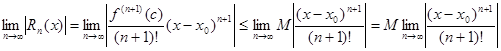Осталось показать, что 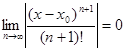. Для этого рассмотрим ряд 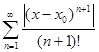. Так как 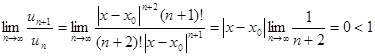, то признаку Даламбера этот ряд сходится на всей числовой оси. Но тогда, в силу необходимости признака сходимости, 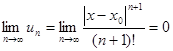. Следовательно, 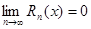. Ч.т.д.

Алгоритм разложения функции f(x) в ряд Маклорена, нужно:

1. найти производные;

2. вычислить значения производных в точке х₀=0;

3. написать ряд (3) для заданной функции и найти его интервал сходимости;

4. найти интервал (-R;R), в котором остаточный член ряда Маклорена 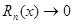при 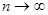. Если такой ряд существует, то в нем функция f(x) и сумма ряда Маклорена совпадают.

Замечание: В интервале сходимости степенного ряда остаточный член стремиться к нулю при .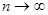

Таблица разложений некоторых элементарных функций в рядэ

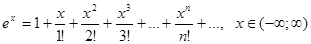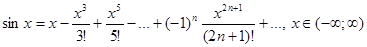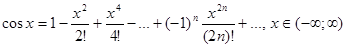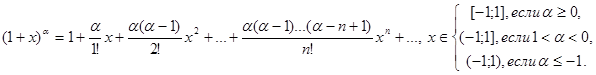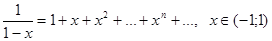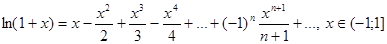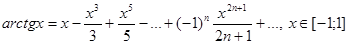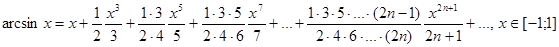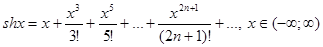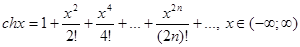Доказательство. Разложить в ряд функцию .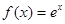

Имеем:

1)

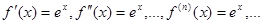
2)

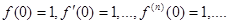
3) применить формулу Маклорена: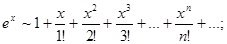

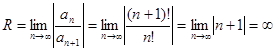, т.е. ряд сходится в интервале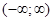

4) для всех ч имеем 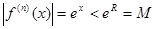, т.е. все производные в этом интервале ограничены одним и тем же числом 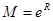. Следовательно, по теореме .

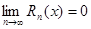Таким образом,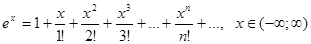

Доказательство. Разложить в ряд функцию .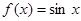

1)

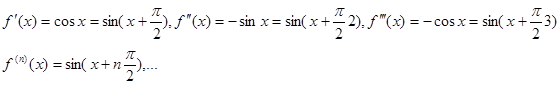
2)

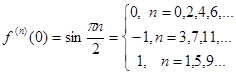
3) применить формулу Маклорена: 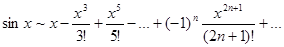, полученный ряд сходится на всей числовой прямой, т.е.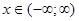

4) любая производная функции по модулю не превосходит единицы, 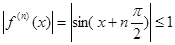. Следовательно, по теореме имеем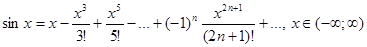

Доказательство. Разложить в ряд функцию .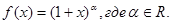

1)

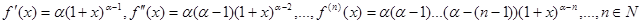
2)

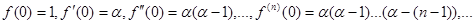
3) применить формулу Маклорена:

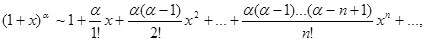
4) 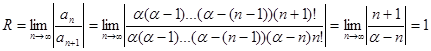, т.е. составленный для функции ряд сходится в интервале (-1;1).

Замечание: Ряд 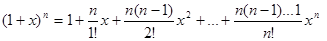называется биномиальным.

Доказательство. Разложить в ряд функцию 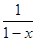. (методом алгебраического деления)

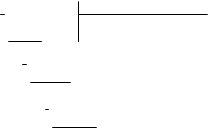Суть метода алгебраического деления состоит в применении общего правила деления многочленов: 1 1 - x

1 – x 1 + x + x² + x³ + …

x

x – x²

x²

x² – x³

x³

……….