Доказательство. Пусть ряд Тейлора сходится к функции f(x) в некоторой окрестности точки х0, т.е

Пусть ряд Тейлора сходится к функции f(x) в некоторой окрестности точки х₀, т.е. 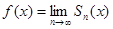. Так как n-я частная сумма S_n(x) ряда Тейлора совпадает с многочленом Тейлора P_n(x), т.е. S_n(x)=P_n(x), находим:

.

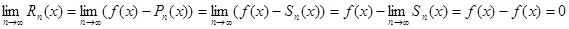Обратно, пусть 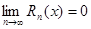. Тогда

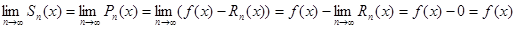. Ч.т.д.

Вывод: Таким образом, задача разложения функции f(x) в степенной ряд сведена по существу к определению значения х, при котором .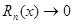

Теорема (достаточное условие разложимости функции в ряд Тейлора). Если модули всех производных функций f(x) ограничены в окрестности точки х₀ одним и тем же числом М>0, то для любого х из этой окрестности ряд Тейлора функции f(x) сходится к функции f(x), т.е. имеет место разложение (2).