2015-06-26
2468
Замечание 2. В разд. 2 и 3 методических указаний приняты следующие обозначения и условия:
одна или две звездочки рядом с номером задачи означают ее сложность;
в условиях задач звездочка заменяет какую-то пропущенную цифру; если в примере используется несколько звездочек, то они могут обозначать разные цифры (например, запись ** означает двузначное число, записанное не обязательно одинаковыми цифрами);
иногда, когда это очевидно, индекс, указывающий на основание системы счисления, не записывается.
П р и м е р 1.
Один преподаватель на вопрос, много ли у него студентов в группе, ответил: «У меня в группе 100 студентов, из них 24 девушки и 21 юноша». В какой системе счисления дал ответ преподаватель?
Решение этой задачи несложное. Пусть р – основание системы счисления, о которой идет речь. Тогда в группе студентов 1·р2 + 0·р1 + 0·р0, из них 2·р1 + 4·р0 девушек и 2·р1 + 1·р0 юношей. Таким образом,
р2 = 2р + 4 + 2р + 1, (8)
или
р2 – 4р – 5 = 0, (9)
отсюда
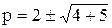, (10)
т. е.
р1 = 5; р2 = –1.
Так как –1 не может быть основанием системы счисления, то единственное решение этой задачи – основание системы счисления р = 5. В группе 25 человек, из них 14 девушек и 11 юношей.
Решить эту задачу можно гораздо проще, если записать:
24р + 21р = 100р.
При сложении цифр 4 и 1 в разряде единиц получился ноль, значит, сумма 4 + 1 = 510 в этой системе счисления дала переполнение и перенос единицы в старший разряд. В любой системе счисления основание записывается как 10р (см. п. 1.2.2). Значит, р = 510.
Ответ: основание системы счисления р = 5.
П р и м е р 2*.
Полным квадратом называется число, которое является квадратом натурального числа. Например, полные квадраты числа 1, 4, 9, 16, 25 и т. д. Существует ли система счисления, в которой число 123р будет полным квадратом?
Развернутая запись числа 123р имеет вид:
1·р2 + 2·р1 + 3·р0. (11)
Запишем выражение (11) иначе:
р2 + 2р + 3, (12)
или
р2 + 2р + 1 + 2, (13)
или
(р + 1)2 + 2. (14)
Выражение (14) не может быть полным квадратом, так как (р + 1)2 – полный квадрат, а из рассмотрения чисел 1, 4, 9, 16, 25, … следует, что не существует полных квадратов, разность между которыми равна двум.
Ответ: такой системы счисления не существует.
П р и м е р 3.
Найти первое слагаемое и сумму, а также основание системы счисления, в которой справедливо соотношение:
***р + 1р = ****р.
Решение задачи очевидно. В любой системе счисления с основанием р прибавление единицы к трехзначному числу дает в результате четырехзначное число только тогда, когда все цифры трехзначного числа одинаковы и равны максимальному значению (р – 1). Если хотя бы одна из цифр трехзначного числа меньше (р – 1), то суммой будет трехзначное число.
Например, 1112 + 12 = 10002; 2223 + 13 = 10003; 7778 + 18 = 10008 и т. д.
Ответ: р – любое натуральное число, большее единицы; первое слагаемое состоит из трех одинаковых цифр, равных (р – 1); сумма двух слагаемых 1000р = р310.
П р и м е р 4.
Найти сумму:
10101,112 + 123,38 + А0,816.
Результат представить в десятичной системе счисления.
Дать два варианта решения:
1) найти сумму в двоичной системе счисления, перевести ее в шестнадцатеричную систему счисления, а затем – в десятичную;
2) сначала все слагаемые перевести в десятичную систему счисления, а потом уже провести суммирование.
1-й вариант
Переведем слагаемые 123,38 и А0,816 в двоичную систему счисления, заменив каждую восьмеричную цифру триадой двоичных цифр, а каждую шестнадцатеричную – тетрадой (см. табл. 2):
123,38 = 001 010 011, 0112;
А0,816 = 1010 0000, 10002.
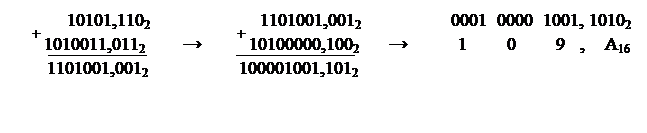Проще сложить сначала первые два слагаемых, а потом к результату прибавить третье:
Переведем окончательный результат в десятичную систему счисления:
109,А16 = 1·162 + 0·161 +9·160 + 10·16–1 = 265,62510.
2-й вариант
Переведем все три слагаемых в десятичную систему счисления:
10101,112 = 1·24 + 0·23 + 1·22 + 0·21 + 1·20 + 1·2-1 + 1·2-2 = 21,7510;
123,38 = 1·82 + 2·81 + 3·80 + 3·8–1= 83,37510;
А0,816 = 10·161 + 0·160 + 8·16–1 = 160,510;
21,75 + 83,375 + 160,5 = 265,625.
Результаты вычислений в обоих вариантах совпали, что подтверждает правильность решения.
Ответ: 265,62510.
П р и м е р 5*.
Найти алгебраическую сумму:
1203 – 322,24.
Дать два варианта решения (см. пример 4).
1-й вариант
Переведем уменьшаемое 1203 и вычитаемое 322,24 в двоичную систему счисления.
Перевод уменьшаемого выполним по схеме (см п. 1.7.1):
A3 → A10 → A2.
1203 = 1·32 + 2·31 + 0·30 = 1510, т. е. А10 = 15.
Для перевода числа 1510 в двоичную систему счисления необходимо выполнить последовательное деление на 2 и выписывание остатков в порядке, обратном их получению (см. п. 1.6.1):
_ 15 | 2 0
10 _ 7 | 2 0
1 4 _ 3 | 2 0
1 2 _ 1 | 2 0
1 0 0 0
Получили запись уменьшаемого в двоичной системе счисления: 11112.
Вычитаемое 322,24 записано в четверичной системе счисления, для перевода его в двоичную систему следует воспользоваться схемой
A4 → A10 → A
и учесть, что 22 = 4. Двоичная и четверичная системы являются системами с кратными основаниями. При переводе числа из шестнадцатеричной системы в двоичную каждую шестнадцатеричную цифру заменим группой из четырех двоичных цифр (тетрадой). При переводе числа из восьмеричной системы в двоичную каждую восьмеричную цифру заменим группой из трех двоичных цифр (триадой). По аналогии при переводе числа из четверичной системы в двоичную каждую четверичную цифру заменим группой из двух двоичных цифр (диадой):
А4 = 3 2 2, 24
А2 = 11 10 10, 102.
Получили запись вычитаемого в двоичной системе счисления: 111010,102.
 |
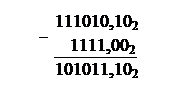Вычитаемое больше уменьшаемого, поэтому (см. п. 1.3.2) вычтем из большего числа меньшее, полученному результату присвоим знак «минус»:
и переведем результат в десятичную систему счисления:
А2 = 1·25 + 0·24 + 1·23 + 0·22 + 1·21 + 1·20 + 1·2-1 = 43,510.
Добавим знак «минус» и получим: – 43,510.
2-й вариант
Число 1203 равно 1510. Переведем число 322,24 в десятичную систему счисления:
322,24 = 3·42 + 2·41 + 2·40 + 2·4-1 = 58,510.
1510 – 58,510 = – 43,510.
Ответ: – 43,510.
П р и м е р 6.
Вычислить:
110111,1012: 54,48 · 2В,816.
Вычисления провести в двоичной системе счисления, а результат за-писать в десятичной.
Переведем числа 54,48 и 2В,816 в двоичную систему счисления (см. табл. 2):
54,48 = 101 100, 1002 = 101100,12;
2В,816 = 0010 1011, 10002 = 101011,12.
Выполним деление, при этом перенесем запятую в делимом и делителе на один разряд вправо, чтобы делимое стало натуральным числом (см. п. 1.3.2):
– 1101111,012 | 10110012
101100100 1,012
– 1011001
10110010
Выполним умножение, предварительно переставив сомножители для упрощения записи (в числе 1,012 меньше цифр, чем в числе 101011,12, поэтому частичных произведений при умножении столбиком будет меньше):
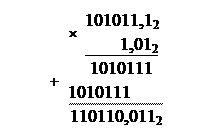
Выполним перевод по схеме:
А2 → А8 → А10.
110110,0112 = 110 110, 0112 = 66,38 = 6·81 + 6·80 + 3·8-1 = 54,37510.
Ответ: 54,37510.
П р и м е р 7*.
Значения длин сторон треугольника заданы числами: 111102, 508, 3216. Определить радиус описанной окружности.
Переведем длину каждой стороны в десятичную систему счисления:
111102 = 3010; 508 = 4010; 3216 = 5010.
Заметив, что 302 + 402 = 502, делаем вывод о том, что треугольник с такими сторонами является прямоугольным с катетами 30, 40 и гипотенузой 50. Тогда диаметр описанной окружности равен гипотенузе прямоугольного треугольника (по школьному курсу математики), а радиус – половине диаметра.
Ответ: радиус описанной окружности равен 25.
3. Задания
З а д а н и е 1. Записать год, месяц, число своего рождения с помощью римских цифр.
З а д а н и е 2. Выписать алфавиты в пятеричной, семеричной и двенадцатеричной системах счисления.
З а д а н и е 3. Записать первые 20 чисел натурального числового ряда в четверичной (табл. 1), пятеричной, семеричной системах счисления.
При выполнении задания следует для получения очередного числа прибавлять единицу к предыдущему числу.
З а д а н и е 4. Записать наименьшее и наибольшее трехзначное в двоичной, троичной, четверичной, пятеричной, семеричной, восьмеричной и шестнадцатеричной системах счисления.
З а д а н и е 5. Выписать целые десятичные числа, принадлежащие следующим числовым отрезкам:
[1102; 10012], [103; 223], [124; 214], [125; 205], [678; 718], [AFF16; B0216].
З а д а н и е 6. Определить, существуют ли системы счисления, в которых выполняются соотношения:
1) *00 + ** = ****;
2) 7**3 + **4 = 7**0.
З а д а н и е 7. Составить небольшие примеры, подтверждающие, что умножение двоичного числа на 2к – переносу запятой в этом числе на к разрядов вправо, а деление двоичного числа на 2к эквивалентно переносу запятой в этом числе на к разрядов влево (см. п. 1.3.2).
З а д а н и е 8. Даны два десятичных числа: 0,210 и 0,310. Выполнить сложение этих чисел дважды:
а) сложением в десятичной системе счисления;
б) переводом каждого из них в двоичную систему счисления с точностью до пяти цифр после запятой, сложением в двоичной системе счисления и переводом результата в десятичную систему счисления.
Результаты вычислений объяснить.
З а д а н и е 9. Перевести смешанную простую дробь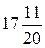 
в двоичную
систему счисления с точностью до четырех цифр после запятой. Результат перевести в десятичную систему и сравнить с исходным числом.
З а д а н и е 10. Данные для выполнения этого задания приведены по вариантам в табл. 3.
1. Выбрать десятичное число и выполнить преобразования по схеме:
а) А10 → А2 → А8 → А10;
б) А10 → А2 → А16 → А10.
2.* Выбрать двоичное число и выполнить преобразования по схеме:
А 2→ А4 → А16 → А10 → А2.
3.* Выбрать шестнадцатеричное число и выполнить преобразования по схеме:
А16 → А4 → А10 → А2 → А16.
4.** Выбрать восьмеричное число и выполнить преобразования по схеме:
А8 → А4 → А10 → А2 → А8.
5. Сложить в двоичной системе счисления двоичное и восьмеричное числа. Результат проверить сложением этих чисел в десятичной системе счисления и переводом его в двоичную систему.
6. Вычесть в двоичной системе счисления из восьмеричного числа шестнадцатеричное число. Полученное число перевести в десятичную систему. Результат проверить вычитанием этих чисел в десятичной системе счисления.
7. Умножить восьмеричное число на шестнадцатеричное число А,816. Умножение выполнить в двоичной системе счисления. Результат проверить переводом обоих сомножителей в десятичную систему счисления и выполнением умножения в этой системе.
8. Разделить шестнадцатеричное число на 10,12. Деление выполнить в двоичной системе счисления. Результат проверить переводом делимого и делителя в десятичную систему счисления и выполнением деления в этой системе.
Т а б л и ц а 3
Исходные данные к заданию 10
| Номер варианта | Ч и с л о в системе счисления | |||
| двоичная | восьмеричная | десятичная | шестнадцатеричная | |
| 101010,011 | 172,2 | 31,750 | АВ,4 | |
| 100000,101 | 213,4 | 29,250 | АF,8 | |
| 110000,111 | 123,4 | 32,500 | BB,C | |
| 101010,001 | 200,4 | 41,250 | BA,4 | |
| 100100,100 | 161,1 | 36,125 | AF,8 | |
| 101000,100 | 211,1 | 42,750 | B4,4 | |
| 111100,100 | 150,4 | 39,625 | BB,C | |
| 110011,010 | 231,4 | 33,375 | AC,C | |
| 111111,100 | 177,2 | 27,500 | BA,8 | |
| 100000,110 | 165,4 | 32,375 | BB,8 | |
| 101111,100 | 201,4 | 27,750 | 1F,2 | |
| 101000,001 | 202,4 | 30,750 | 97,8 | |
| 111100,010 | 166,2 | 35,500 | 9F,4 | |
| 111110,001 | 136,4 | 44,500 | AE,C | |
| 101011,100 | 232,2 | 40,375 | BE,4 | |
| 111001,010 | 155,4 | 33,250 | AA,8 |
Контрольные вопросы
1. В римской системе счисления записаны два числа: MXM и MMX. Какое число больше?
2. Какое количество обозначает цифра 2 в числах 2023, 20213, 2024, 20214, 2025, 20215, 2027, 20217, 2028, 20218, 20210, 202110, 20212, 202112, 20216, 202116?
3. Какое число предшествует и какое число следует за каждым из данных: 1011012, 1203, 1304, 2105, 3007, 2008, 3012, 2016? Ответ дать в заданной и десятичной системах счисления.
4. Существует ли система счисления, в которой десятичное число 15 будет оканчиваться цифрой 7?
5. В какой системе счисления с основанием р десятичное число 16 записывается как 17р, а в какой как 20р?
6. Какое число больше: 1234 или 1235; 7778 или FF16?
7. Каково соотношение между р и q, если известно, что 400р = 100q?
8. Существуют ли системы счисления, в которых выполняются соотношения: а) 16р + 12р = 40р; б) 16р + 12р = 31р; в) 2р . 2р = 3р; г) 12р – 6р = 5р;
д) 100р: 2р = 20р?
9. В какой системе счисления с выполнено вычитание: ***р – 1 = **р?
10*. Существует ли система счисления, в которой десятичное число 15 будет оканчиваться цифрой 0, двумя нулями?
11*. Какое число больше: ааар или аааq, если известно, что а – какая-то арабская цифра, а натуральное число р меньше натурального числа q?
12*. Существует ли система счисления, в которой число 17р будет полным квадратом?
13*. Каково минимальное основание системы счисления, в которой число 13р будет полным квадратом?
14**. Существует ли система счисления, в которой десятичное число 50 будет оканчиваться двумя нулями?
15**. Существует ли система счисления, в которой двузначное число, записанное с помощью двух одинаковых цифр, будет полным квадратом?
16**. Существует ли система счисления с основанием отличным от 10, в которой число 144р будет полным квадратом?
1. Информатика. Базовый курс / С. В. С и м о н о в и ч, Г. А. Е в с е е в
и др. СПб: Питер, 2005. 640 с.
2. Информатика / Под. ред. проф. Н. В. Макаровой. М.: Финансы и статистика, 2001.768 с.
3. В е р е т е н н и к о в а Е. Г. Информатика / Серия «Учебный курс». /
Е. Г. В е р е т е н н и к о в а, С. М. П а т р у ш и н а, Н. Г. С а в е л ь е в а.
Ростов-на-Дону: МарТ, 2002. 416 с.
Учебное издание
СОКОЛОВСКАЯ Нина Николаевна
