Требуется найти такие значения 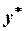 и
и 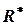 , при которых функция общих суммарных затрат в единицу времени
, при которых функция общих суммарных затрат в единицу времени
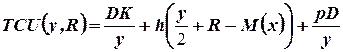
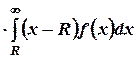
принимает минимальное значение.
Решение. В соответствии с необходимым условием существования экстремума функции нескольких переменных, находим частные производные
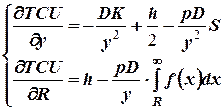
Находим стационарные точки, решая систему уравнений:
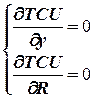
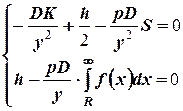
Находим оптимальные значения 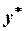 и
и 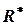
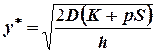 (1)
(1)
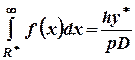 (2)
(2)
Так как из уравнений (1) и (2) нельзя определить в явном виде оптимальные значения 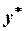 и
и 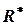 , то для их нахождения используется численный алгоритм, предложенный Хедли и Уайтин. Ими было доказано, что итерационный алгоритм вычисления оптимальных значений
, то для их нахождения используется численный алгоритм, предложенный Хедли и Уайтин. Ими было доказано, что итерационный алгоритм вычисления оптимальных значений 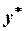 и
и 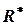 сходится за конечное число итераций при условии, что допустимое решение существует.
сходится за конечное число итераций при условии, что допустимое решение существует.
Алгоритм Хедли - Уайтин.
Полагая 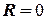 , из уравнений (1) и (2) находим значения:
, из уравнений (1) и (2) находим значения:
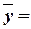
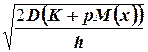
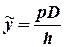 .
.
Если 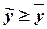 , то вычисляется наименьшее значением
, то вычисляется наименьшее значением 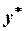 =
= 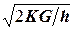 , которое достигается при
, которое достигается при 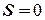 . Затем оптимальные значения
. Затем оптимальные значения 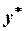 и
и 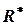 определяются единственным образом с помощь следующей итерационной процедуры.
определяются единственным образом с помощь следующей итерационной процедуры.
Итерация 0. Принимаем начальное решение 
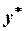 =
= 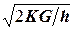 и
и 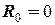 Полагаем
Полагаем 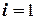 и переходим к шагу
и переходим к шагу 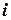 .
.
Итерация 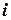 . Используем значение
. Используем значение 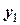 для определения
для определения 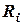 , из уравнения (2). Здесь возможны два случая;
, из уравнения (2). Здесь возможны два случая;
- Если
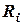 =
= 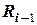 , то вычисления заканчиваются; оптимальным решением считаем
, то вычисления заканчиваются; оптимальным решением считаем 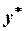 =
= 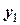 и
и 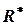 =
= 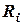 .
.
2. Если 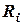
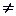
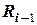 , то вычисления продолжаются. Используем значение
, то вычисления продолжаются. Используем значение 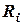 , в уравнении (1) для вычисления
, в уравнении (1) для вычисления 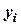 . Полагаем
. Полагаем 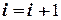 и повторяем итерацию
и повторяем итерацию 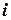 .
.
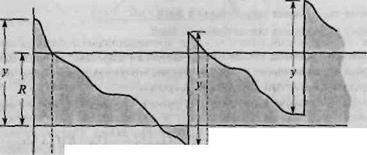
В стохастической модели экономического размера заказа допускается неудовлетворенный спрос, как это показано на рис. 3.
.
Рис. 3.
 2015-06-26
2015-06-26 630
630








