2015-06-26
476
При условии, что дневной спрос является нормально распределенной случайной величиной с математическим ожиданием D = 100 ламп и среднеквадратическим отклонением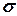 
= 10 ламп, требуется определить оптимальный размер страхового запаса, при котором вероятность истощения запаса в течение периода выполнения заказа не превышает величины 
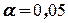. Совокупные затраты по закупке и хранению запасов на складе должны быть минимальны.
Решение. При решении иллюстративной задачи 1 был определен оптимальный размер заказа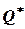 
=1000 ламп и эффективное время выполнения заказа 
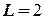дня.
Определим теперь дневной спрос, который является нормально распределенной случайной величиной с математическим ожиданием D = 100 ламп и среднеквадратическим отклонением 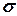= 10 ламп. Находим
= 
= 
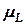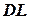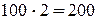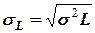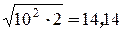ламп,
= 
ламп.
Рассмотрим теперь вероятностное условие
.
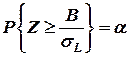Т.к. по условию 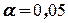, то из условия
,
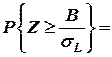
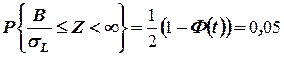находим
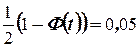
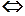
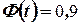
С помощью таблиц функции Лапласа находим
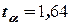
Следовательно, размер резервного запаса вычисляется следующим образом.
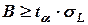
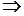
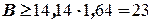неоновые лампы.
Вывод: при экономичном размере заказа 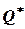= 1000 ламп оптимальная стратегия управления запасами с объемом резерва В состоит в заказе 1000 ламп, как только объем запаса уменьшается до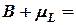 
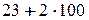= 223 неоновых ламп.
