Для построения модели вводим обозначения:
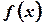 — плотность распределения спроса
— плотность распределения спроса 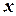 в течение периода выполнения заказа,
в течение периода выполнения заказа,
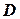 — среднее значение спроса в единицу времени,
— среднее значение спроса в единицу времени,
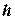 — удельные затраты на хранение (затраты на хранение единицы продукции в течение единицы времени),
— удельные затраты на хранение (затраты на хранение единицы продукции в течение единицы времени),
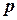 — удельные потери от неудовлетворенного спроса (потери на единицу продукции за единицу времени),
— удельные потери от неудовлетворенного спроса (потери на единицу продукции за единицу времени),
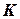 — стоимость размещения заказа.
— стоимость размещения заказа.
В рассматриваемой модели заказ размером 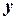 размещается тогда, когда объем запаса достигает уровня
размещается тогда, когда объем запаса достигает уровня 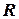 . Как и в детерминированном случае, уровень
. Как и в детерминированном случае, уровень 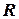 , при котором размешается заказ, является функцией периода времени между размещением заказа и его выполнением. Оптимальные значения
, при котором размешается заказ, является функцией периода времени между размещением заказа и его выполнением. Оптимальные значения 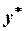 и
и 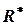 определяются путем минимизации ожидаемых затрат системы управления запасами, отнесенных к единице времени, которые включают как расходы на размещение заказа и его хранение, так и потери, связанные с неудовлетворенным спросом.
определяются путем минимизации ожидаемых затрат системы управления запасами, отнесенных к единице времени, которые включают как расходы на размещение заказа и его хранение, так и потери, связанные с неудовлетворенным спросом.
Основываясь на этих предположениях, вычислим компоненты функции затрат.
1. Стоимость размещения заказов. Приближенное число заказов в единицу времени равно 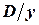 , так что стоимость размещения заказов в единицу времени равна
, так что стоимость размещения заказов в единицу времени равна 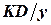 .
.
2. Ожидаемые затраты на хранение. Усредняя ожидаемые уровни запасов в начале и конце периода выполнения заказа, получаем, что средний уровень запаса определяется по формуле
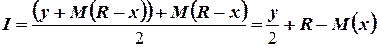 .
.
Следовательно, ожидаемые затраты на хранение за единицу времени равны 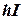 .
.
Отметим, что при рассмотрении модели игнорируется случай, когда величина 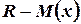 отрицательна, что является одним из упрощающих допущений рассматриваемой модели.
отрицательна, что является одним из упрощающих допущений рассматриваемой модели.
3. Ожидаемые потери, связанные с неудовлетворенным спросом. Дефицит возникает при 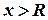 . Следовательно, дефицит, ожидаемый в течение единицы времени, равен
. Следовательно, дефицит, ожидаемый в течение единицы времени, равен
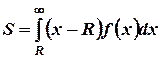 .
.
Так как в модели предполагается, что 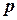 пропорционально лишь объему дефицита, то ожидаемые потери, связанные с неудовлетворенным спросом, за один цикл равны
пропорционально лишь объему дефицита, то ожидаемые потери, связанные с неудовлетворенным спросом, за один цикл равны 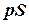 . Поскольку единица времени содержит
. Поскольку единица времени содержит 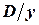 циклов, то ожидаемые потери, обусловленные дефицитом, составляют
циклов, то ожидаемые потери, обусловленные дефицитом, составляют 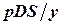 за единицу времени.
за единицу времени.
Результирующая функция, отражающая суммарные затраты за единицу времени 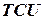 , имеет следующий вид.
, имеет следующий вид.
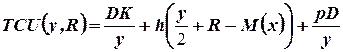
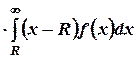 .
.
 2015-06-26
2015-06-26 483
483








