Простейшая модель и формулы Уилсона

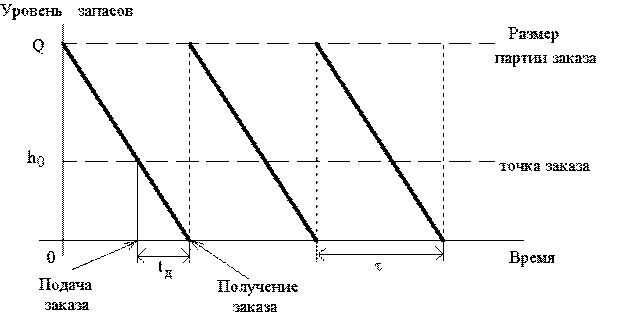
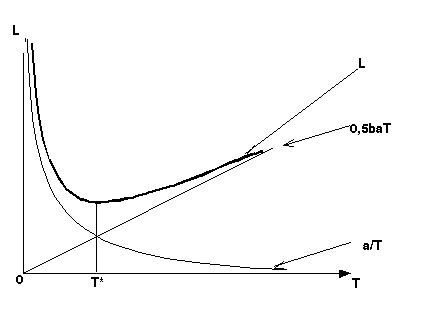
n - объем одной поставляемой партии;

T - интервал между поставками (цикл);

b - интенсивность расходования запасов;

с₁ - затраты на доставку, не зависящие от объема партии (организационные издержки);

с₂ - затраты на хранение единицы продукта в единицу времени;

N - общее потребление запасаемого продукта за общий интервал времени работы.

Общие затраты С определяются суммой затрат на поставку и хранение:

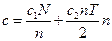
Оптимальный объем партии ;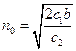

Длительность цикла ;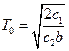

Оптимальные средние затраты в единицу времени -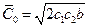

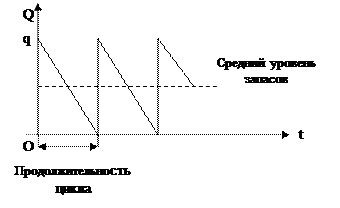
Пример 1. Интенсивность равномерного спроса составляет 2000 телевизоров в год. Организационные издержки для одной партии составляют 20 тыс.р. Цена единицы товара равна 1 тыс.р., а издержки содержания телевизоров составляют 0,1 тыс.р. за один телевизор в год.

Найти оптимальный размер партии (q), число поставок (n) и продолжительность цикла (t).

РЕШЕНИЕ.

Обозначим:

g – годовой спрос; g = 2000

b – организационные издержки; b = 20

s – цена товара; s = 1

h – издержки содержания запасов; h = 0,1

Общие издержки в течение года:

С = С₁ + С₂ + С₃,

где С₁ – общие организационные издержки; С₂ – стоимость товаров; С₃ – общие издержки содержания запасов.

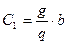, где 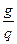- количество партий; ;

; ;

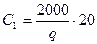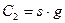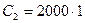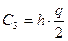, где 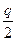- среднее количество запасов на складе.

Имеем .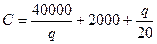

Найдём 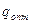, чтобы издержки С были минимальными.

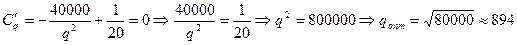ед.

п – число поставок; 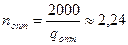; 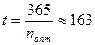дня.

ОТВЕТ. Оптимальный размер партии составляет 894 телевизора; число поставок – 2,24; продолжительность цикла – 163 дня.