Проективное отображение

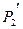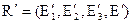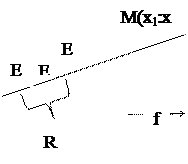
Определение 1: пусть на проективных плоскостях P₂ и заданы соответственно проективные системы координат (реперы) R=(Е₁,Е₂,Е₃,Е) и . Отображение f точками P₂ на плоскость 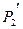называется проективным отображением или коллинеацией, если оно любую точку М с координатами х₁:х₂:х₃ в репере R отображаем на точку 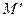с такими же координатами в репере .

.

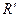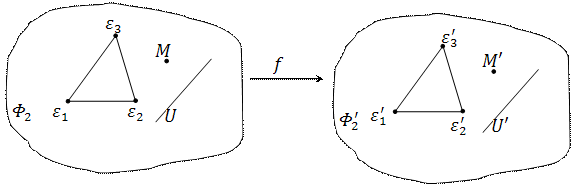
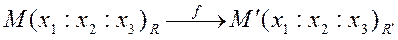ЗАМЕЧАНИЯ: 1) проективное отображение 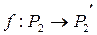является взаимно однозначным (биективным);

2) при f точки Е₁,Е₂,Е₃,Е отображаются соответственно на точки 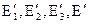, то есть репер R отображается на репер : ;

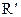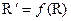3) проективное отображение f вполне определяется заданием координатных реперов R и .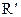

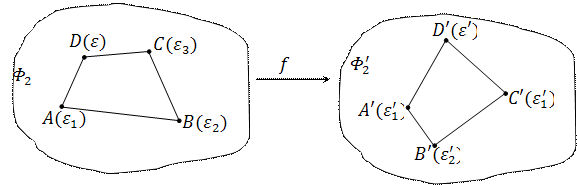Вообще говоря, это отображение вполне определяется заданием любых двух соответствующих реперов, то есть заданием двух соответствующих четырехвершинников ABCD и :

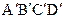Теорема: проективное отображение f любую прямую u проективной плоскости P₂ переводит в некоторую прямую u’ проективной плоскости P₂’.

Доказательство: пусть на проективной плоскости P₂ задана проективная прямая u своим уравнением относительно репера R:

u₁x₁+u₂x₂+u₃x₃=0 (*)

Пусть 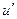=f(u) и 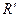=f(R) – образы прямойu и репера R при отображении f. Так как координаты точек в системе 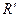совпадают при коллинеацииf с координатами их прообразов в системе R, то фигура 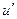задается в репере 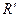тем же самым уравнением (*). Тогда образ 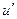прямой u при коллинеацииf будет также некоторой прямой линией проективной плоскости .

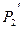Замечания:

4. Справедлива и обратная теорема: «отображение f: P₂→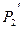, при котором прямая переходит в прямую, является проективным отображением (коллинеацией)». Следовательно, коллинеацию можно определить как отображение переводящее прямую в прямую (сохраняющее прямолинейность точек). Отсюда и происходит название «коллинеация».

5. Проективное отображение проективной прямой P₁ на проективную прямую 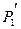определяется аналогично:

E1’ E’ E2’

M’(x1:x2)

R

R’

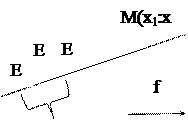Это отображение вполне определяется заданием двух соответствующих реперов R и R’, то есть двух троек (упорядоченных соответствующих точек А, В, С и A’, B’, С’.

		E1’ E’ E2’		M’(x1:x2)

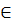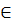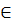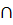Определение: пусть p и p’– две различные прямые проективной плоскости P₂ и точка Q – точка этой плоскости, на них не лежащая. Отображение прямой p на прямую p’ называется перспективным отображением или центральным проектированием, если образом точки Mp служит M’p’ такая, что M’=QMp’.

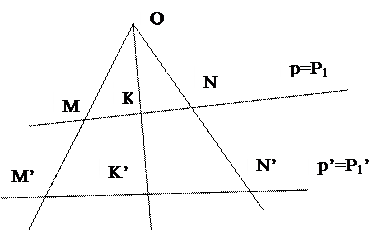
Точка Q называется центром перспективы или центром проектирования.

Замечание:

6. Можно доказать, что перспективное отображение прямой является частным случаем проективного отображения.