15.1. Определение криволинейного интеграла по длине дуги и его свойства:
Пусть 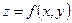 непрерывна в каждой точке гладкой дуги
непрерывна в каждой точке гладкой дуги 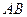 .
.
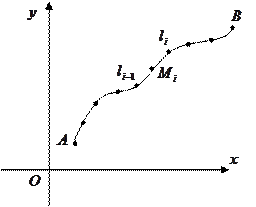
 Определение:
Определение:
Конечный предел интегральной суммы функции 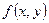 на кривой
на кривой 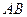 при условии, что
при условии, что 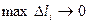 и
и 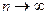 называется криволинейным интегралом по длине дуги от функции
называется криволинейным интегралом по длине дуги от функции 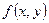 по кривой
по кривой 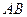 , где
, где 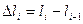
Т.о. 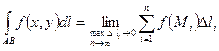 .
.
Основные свойства:
1) 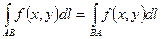 ;
;
2) 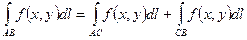 ;
;
3) Если в каждой точке дуги 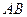
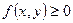 , то и
, то и 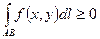 ;
;
4) Если в каждой точке дуги 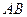
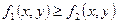 , то и
, то и 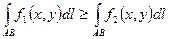 ;
;
5) 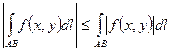 ;
;
6) 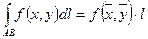 , где
, где 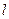 - длина дуги
- длина дуги 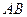 ,
, 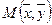 - точка дуги.
- точка дуги.
15.2 Вычисление криволинейных интегралов по длине дуги:
· 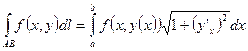 - в случае явного задания кривой интегрирования
- в случае явного задания кривой интегрирования 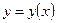 ;
;
· 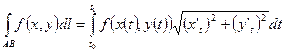 - в случае параметрического задания кривой интегрирования
- в случае параметрического задания кривой интегрирования 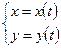 ;
;
· 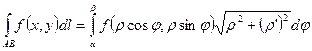 - в случае задания кривой интегрирования в п.с.к.
- в случае задания кривой интегрирования в п.с.к. 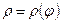 .
.
15.3 Применения криволинейного интеграла по длине дуги:
· 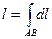 - длина дуги;
- длина дуги;
· 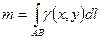 - масса неоднородной дуги с плотностью
- масса неоднородной дуги с плотностью 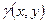 ;
;
· 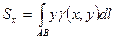 ;
; 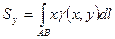 - стат. моменты дуги относительно коорд. осей;
- стат. моменты дуги относительно коорд. осей;
· 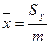 ;
; 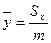 - координаты центра масс дуги;
- координаты центра масс дуги;
· 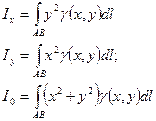 - моменты инерции дуги.
- моменты инерции дуги.
15.4 Криволинейный интеграл по координатам:
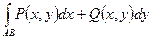 - составной криволинейный интеграл.
- составной криволинейный интеграл.
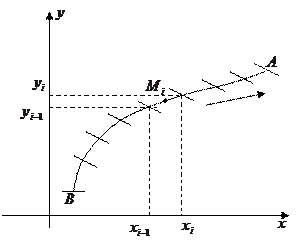
Пусть 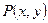 - непрерывна в каждой точке гладкой направленной дуги
- непрерывна в каждой точке гладкой направленной дуги 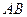 .
.
Определение:
Конечный предел интегральной суммы функции 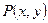 на кривой
на кривой 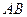 при условии, что
при условии, что 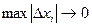 и
и 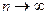 называется криволинейным интегралом по координате
называется криволинейным интегралом по координате  от функции
от функции 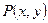 по кривой
по кривой 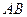 , где
, где 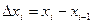
Т.о. 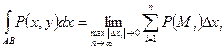 .
.
Аналогично 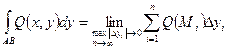 .
.
Основные свойства:
1) 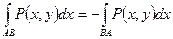 ;
;
2) 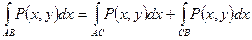 ;
;
3) Криволинейные интегралы по координатам, взятые по замкнутому контуру 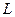 не зависят от выбора на контуре начальной точки, но зависят от направления обхода контура.
не зависят от выбора на контуре начальной точки, но зависят от направления обхода контура.
Если направление обхода не указано, то полагают, что контур обходится в положительном направлении (такое, при котором точки области, ограниченные контуром, остаются слева).
15.5 Вычисление криволинейных интегралов по координатам:
1. 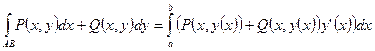 - в случае явного задания кривой интегрирования;
- в случае явного задания кривой интегрирования;
2. 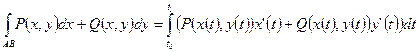 - в случае параметрического задания кривой интегрирования;
- в случае параметрического задания кривой интегрирования;
3. 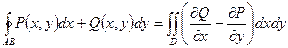 - формула Грина, где
- формула Грина, где 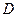 - область, ограниченная контуром
- область, ограниченная контуром 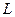 .
.
4. Если 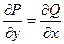 , то
, то 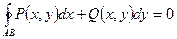 ;
;
5. Если 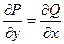 и
и 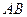 - незамкнутая кривая
- незамкнутая кривая 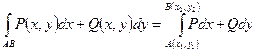 , т.е. вычисление таких интегралов сводится к вычислению определенных, однако, в качестве линии интегрирования удобно брать ломаную, звенья которой параллельны осям координат.
, т.е. вычисление таких интегралов сводится к вычислению определенных, однако, в качестве линии интегрирования удобно брать ломаную, звенья которой параллельны осям координат.
15.6 Применения криволинейных интегралов по координатам:
1. 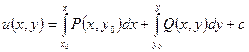 - нахождение функции по ее полному дифференциалу, где
- нахождение функции по ее полному дифференциалу, где 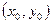 - точка из области непрерывности
- точка из области непрерывности 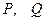 ;
;
2. 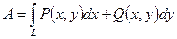 - работа силы
- работа силы 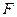 , где
, где 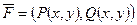 , по перемещению материальной точки
, по перемещению материальной точки 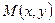 ;
;
3. 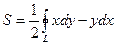 - площадь плоской фигуры.
- площадь плоской фигуры.
Теорема (условие независимости составного интеграла по координатам от формы кривой интегрирования):
Если функции 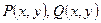 и их частные производные первого порядка непрерывны в некоторой области
и их частные производные первого порядка непрерывны в некоторой области 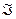 , то для того чтобы составной интеграл по координатам не зависел от формы кривой интегрирования необходимо и достаточно, чтобы в каждой точке области
, то для того чтобы составной интеграл по координатам не зависел от формы кривой интегрирования необходимо и достаточно, чтобы в каждой точке области 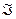 подынтегральное выражение
подынтегральное выражение 
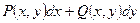 было полным дифференциалом некоторой функции двух переменных
было полным дифференциалом некоторой функции двух переменных 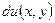 .
.
 2015-06-26
2015-06-26 3960
3960








