Раздел i: обыкновенные дифференциальные уравнения первого порядка

1.1. Основные понятия:

Определение:

Уравнение, содержащее неизвестные функции, их аргументы и производные (дифференциалы) различных порядков от этих функции по своим аргументам называется дифференциальным.

Определение:

Порядком д.у. называется порядок старшей производной или старшего дифференциала функции, входящих в уравнение.

Определение:

Решением д.у. называется всякая функция, обращающая это уравнение в тождество.

1.2. Типы дифференциальных уравнений первого порядка:

1) С разделяющимися переменными:

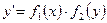
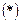- разрешенное относительно производной

Алгоритм решения:

- заменяем 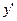на ;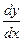

- разделяем переменные: слева с 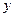, справа с ;

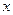- интегрируем уравнение с разделенными переменными;

- записываем общее решение или общий интеграл.

Частный случай : ; .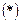

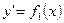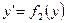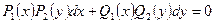- в дифференциальной форме.

Метод решения тотже.

2) Однородные дифференциальные уравнения:

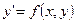, где 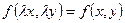- разрешенное относительно производной.

Ход решения:

- вводим новую функцию 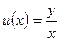или ;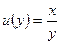

- сводим к уравнению с разделяющимися переменными, интегрируем.

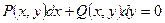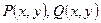( - однородные функции одного измерения) – дифференциальная форма.

3) Линейные дифференциальные уравнения:

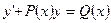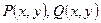Общая форма: , где - непрерывные функции, в частности постоянные.

Признак: 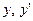входят только в первой положительной степени и нет их произведения 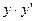, 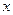- в любой форме.

Ход решения:

- подставляем в данное уравнение ;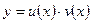

- решаем последовательно два д.у. с разделяющимися переменными: одно д.у. относительно 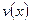, другое относительно ;

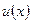- записываем общее решение (общий интеграл).

Еще одна форма линейного дифференциального уравнения: .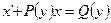

Решаются введением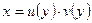

4) Уравнения Бернулли:

Общий вид - 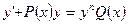, где 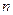- любой действительное число 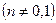, 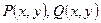- непрерывные функции, в частности постоянные.

Эти уравнения сводят к линейным, поэтому решение его вида .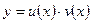

5) Дифференциальные уравнения в полных дифференциалах:

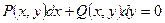, где .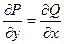

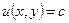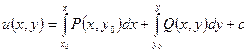Решение ищем в виде , где и 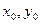- из области непрерывности .

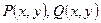1.3. Дифференциальные уравнения высших порядков:

1) Дифференциальные уравнения вида 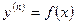, где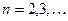

Для нахождения решения последовательно интегрируем заданное д.у. по 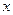столько раз, каков порядок уравнения.

2) Дифференциальные уравнения вида .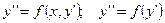

Для нахождения решения вводим новую функцию 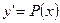, тогда .

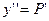Замечание:

- д.у. вида 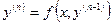, где 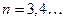решаем с помощью подставки .

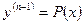3) Дифференциальные уравнения вида .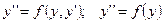

Для нахождения решения вводим новую функцию 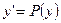, тогда .

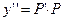4) Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами (ЛОДУ)

Общий вид: .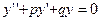

Ход решения:

- составляем характеристическое уравнение вида ;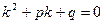

- решаем характеристическое равнение, используя дискриминант;

- записываем общее решение, учитывая:

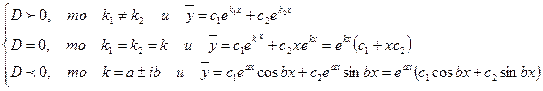
ЛОДУ высших порядков решаются аналогично.

5) Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами (ЛНДУ)

Общий вид 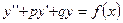, где 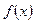- непрерывная функция при всех рассматриваемых .

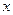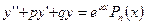- ЛНДУ второго порядка с первой специальной правой частью ( 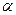- любое действительное число, включая ноль, 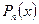- многочлен 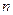-ой степени с действительными коэффициентами)

Его решение имеет вид: 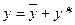, где

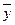- - общее решение соответствующего ЛОДУ ,

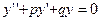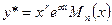- , где 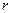- кратность, с которой 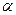входит в число корней характеристического уравнения, 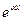- из условия, 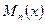- многочлен 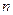- ой степени, взятый с буквенными коэффициентами.

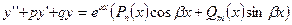- ЛНДУ второго порядка со второй специальной правой частью ( 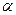- любое действительное число, включая ноль,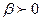 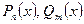- многочлен 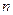-ой и 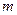- ой степени с действительными коэффициентами)

Его решение имеет вид: 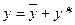, где

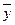- - общее решение соответствующего ЛОДУ ,

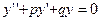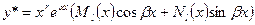- , где 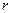- кратность, с которой пара чисел 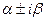входит в число корней характеристического уравнения, 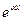- из условия, 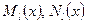- разные многочлены одной степени с буквенными коэффициентами ().

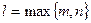ЛНДУ высших порядков решают аналогично.

Теорема:

Если 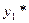- частное решение д.у. 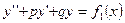, 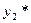- частное решение д.у. 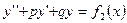, то их сумма 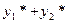- частное решение д.у. .

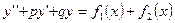6) Метод Лагранжа (для интегрирования ЛНДУ второго и высших порядков)

Этот метод целесообразно применять при интегрировании ЛНДУ с постоянными коэффициентами, но без специальной правой части и уравнений с переменными коэффициетами.

Пусть имеем 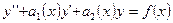- ЛНДУ второго порядка. Найдем его решение в виде 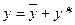методом вариации.

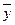- - решение соответствующего ЛОДУ;

- ;

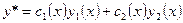- составляем СЛАУ относительно :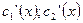

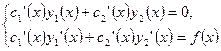
- находим по формулам Крамера решение системы: ;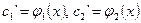

- итнегрируем последнее равенство и полагаем постоянные интегрирования равными нулю, тем самым находим ;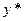

- записываем решение в виде .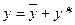

1.4.Системы диффереренциальных уравнений.

Определение:

Система диффереренциальных уравнений вида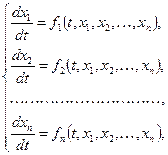

где 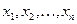- неизвестные функции независимой переменной 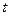, называется нормальной системой.

Если правые части нормальной системы дифференциальных уравнений являются линейными функциями относительно 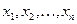, то система дифференциальных уравнений называется линейной.

1) Иногда нормальную систему дифференциальных уравнений удается свести к одному уравнению 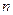- го порядка, содержащему одну неизвестную функцию. Сведение нормальной системы к одному уравнению может быть достигнуто дифференцированием одного из уравнений системы и исключением всех неизвестных, кроме одного.

В некоторых случаях, комбинируя уравнения системы, после несложных преобразований удается получить легко интегрируемые уравнения, что позволяет найти решение системы.

2) Пусть дана система 3 линейных дифференциальных уравнений с 3 неизвестными функциями, коэффициенты которых постоянные:

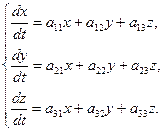
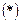
Общее решение имеет вид: .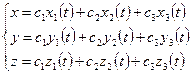

Здесь 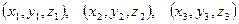- нетривиальные частные решения системы, причем такие, что каждая тройка функций образуют ФСР .

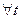Ищем такие частные решения системы в виде 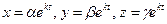, здесь 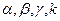- некоторые константы. Подставив значения 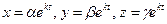в систему дифференциальных уравнений 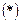, получим систему линейный алгебраических уравнений относительно :

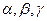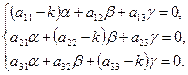
Составляем характеристическое уравнение: .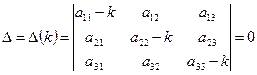

Оно имеет три корня: действительных или комплексно-сопряженных.

- Если корни дейстительные и различные 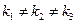, то для каждого корня 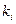находим из системы 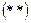одно из ее решений 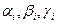вида:

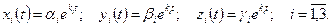
Линейная комбинация полученных частных решений определит общее решение заданной системы.

- Если среди корней есть пара комплексно-сопряженных чисел, т.е. 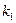- действительное, 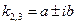, то аналогичным способом с помощью корня 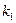находим первое частное решение системы в действительной форме. С помощью корня 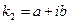или 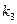получаем новое частное решение в комплексной форме. Выделив в новом решении действительные и мнимые части, составляем из них соответственно частные решения в действительной форме.