 16.1. Определение и свойства поверхностого интеграла по площади поверхности
16.1. Определение и свойства поверхностого интеграла по площади поверхности  :
:
Пусть функция 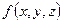 - непрерывна в каждой точке гладкой поверхности
- непрерывна в каждой точке гладкой поверхности  .
.
Определение:
Конечный предел интегральной суммы функции 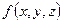 в области
в области  при условии, что
при условии, что 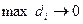 и
и 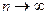 называется поверхностным интегралом по площади поверхности от функции
называется поверхностным интегралом по площади поверхности от функции 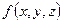 по поверхности
по поверхности  , где
, где 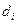 - диаметр частичной поверхности.
- диаметр частичной поверхности.
Т.о. 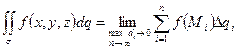 , где
, где 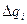 - площадь частичной поверхности.
- площадь частичной поверхности.
Определение:
Сторона поверхности называется положительной (отрицательной) в направлении оси 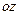 , если нормаль, проведенная к этой стороне в произвольной точке составляет с осью
, если нормаль, проведенная к этой стороне в произвольной точке составляет с осью 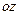 острый (тупой) угол.
острый (тупой) угол.
Аналогично, для 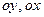 .
.
Определение:
Выбор одной из двух сторон поверхностей (положительной или отрицательной) в направлении определенной оси называется ориентацией поверхности в направлении выбранной оси.
Основные свойства:
- Поверхностные интегралы не завися от ориентации поверхности в направлении любой оси.
-
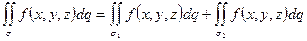 ;
; - Если всюду на

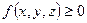 , то и
, то и 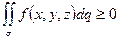 ;
; - Если всюду на

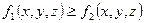 , то и
, то и 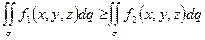 ;
; -
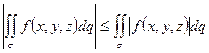 ;
; -
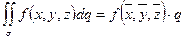 , где
, где 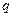 - площадь
- площадь  ,
, 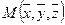 - из поверхности
- из поверхности  .
.
16.2. Вычисление поверхностных интегралов по площади поверхности:
- Выясняем, прямая параллельная какой оси, пересекает эту поверхность не более чем в одной точке;
- Тогда уравнение
 разрешаем относительно этой переменной, проецируем
разрешаем относительно этой переменной, проецируем  на соответствующую двумерную плоскость.
на соответствующую двумерную плоскость.
Т.е., если такая прямая параллельна оси 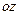 :
:
- уравнение  :
: 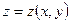 ;
;
- проецируем  на
на 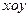 и
и 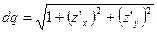 .
.
3. Переходим к двойному интегралу:
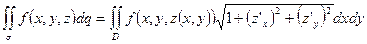 .
.
16.3. Применения поверхностных интегралов по площади поверхности:
· 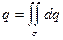 - площадь поверхности
- площадь поверхности  ;
;
· 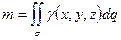 - масса гладкой неоднородной поверхности
- масса гладкой неоднородной поверхности  с плотностью
с плотностью 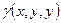 ;
;
· 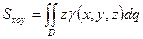 ;
; 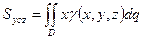 ;
; 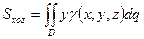 - статические моменты относительно координатных плоскостей;
- статические моменты относительно координатных плоскостей;
· 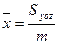 ;
; 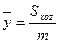 ;
; 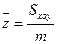 ; - координаты центра масс поверхности;
; - координаты центра масс поверхности;
· 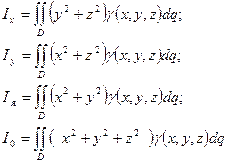 - моменты инерции поверхности относительно координатных осей.
- моменты инерции поверхности относительно координатных осей.
16.4. Определение и свойства поверхностного интеграла по координатам 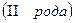 :
:

Пусть имеет гладкую поверхность  , соорентируем ее в направлении оси
, соорентируем ее в направлении оси 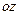 .
.
Положим, что в каждой точке этой поверхности задана непрерывная функция 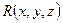 .
.
Определение:
Конечный предел интегральной суммы функции 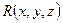 на поверхности
на поверхности  при условии, что
при условии, что 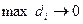 и
и 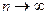 называется поверхностным интегралом по координатам
называется поверхностным интегралом по координатам 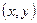 от функции
от функции 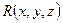 по поверхности
по поверхности  , где
, где 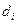 - диаметр частичной поверхности.
- диаметр частичной поверхности.
Т.о. 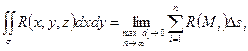 , где
, где 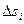 - площадь проекции частичной поверхности на
- площадь проекции частичной поверхности на 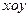 .
.
Аналогично, определяются поверхностные интегралы по координатам 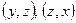 .
.
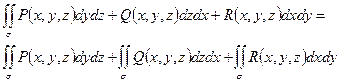 - составной поверхностный интеграл по координатам.
- составной поверхностный интеграл по координатам.
Основные свойства:
1). Каждый из поверхностных интегралов по координатам зависит от ориентации поверхности в направлении соответствующей оси, т.е.
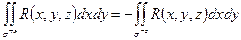
2)Если  - цилиндрическая поверхность с образующей, параллельной оси
- цилиндрическая поверхность с образующей, параллельной оси 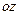 , то
, то 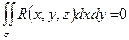 ;
;
3) 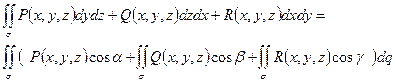 , где
, где 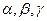 - углы, образованные вектором
- углы, образованные вектором 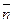 с соответствующими координатными осями.
с соответствующими координатными осями.
16.5. Вычисление поверхностных интегралов по координатам:
1) Выясняем, прямая параллельная какой оси, пересекает эту поверхность не более чем в одной точке;
2) Ориентируем поверхность в направлении этой оси;
3) Уравнение  разрешаем относительно этой переменной, проецируем
разрешаем относительно этой переменной, проецируем  на соответствующую двумерную плоскость.
на соответствующую двумерную плоскость.
4) Переходим к двойному интегралу:
Если такая прямая параллельна оси 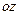 , то уравнение
, то уравнение  :
: 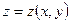 и
и
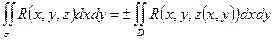 .
.
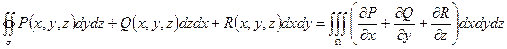 - формула Остроградского-Гаусса.
- формула Остроградского-Гаусса.
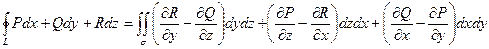 - формула Стокса.
- формула Стокса.
КУРС
 2015-06-26
2015-06-26 653
653








