12.1. Определение и свойства:
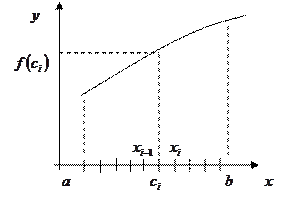

 Определение:
Определение:
Конечный предел интегральной суммы функции 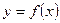 на
на 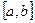 называется определенным интегралом от этой функции на
называется определенным интегралом от этой функции на 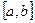 .
.
Т.о. 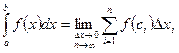 , где
, где 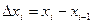 .
.
Теорема (формула Ньютона-Лейбница): Определенный интеграл от непрерывной функции равен разности двух значений любой первообразной подынтегральной функции, взятых при верхнем и нижнем пределах интегрирования: 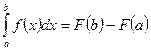 .
.
Основные свойства определенного интеграла:
1) 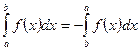 ;
;
2) 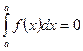 ;
;
3) 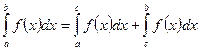 - свойство аддитивности
- свойство аддитивности
4) Если на 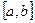 , где
, где 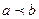
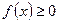 , то и
, то и 
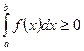 ;
;
5) Интегрирование неравенств:
Если на 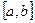 , где
, где 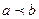
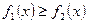 , то и
, то и 
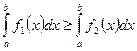 ;
;
6) Об оценке определенного интеграла:
Если 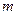 - наименьшее,
- наименьшее, 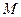 - наибольшее значения функции
- наибольшее значения функции  на
на 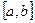 , то
, то
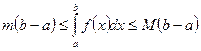 ;
;
7) 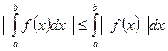 ;
;
8) Теорема о среднем: 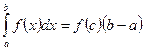 , где
, где 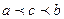
9) 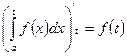 .
.
12.2. Методы вычисления определенного интеграла:
- Непосредственное интегрирование (применение формулы Ньютона-Лейбница);
- Замена переменной интегрирования: 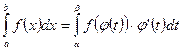 . Здесь не возвращаются к исходной переменной, но сразу вводят новые пределы интегрирования.
. Здесь не возвращаются к исходной переменной, но сразу вводят новые пределы интегрирования.
- Интегрирование по частям: если 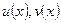 - непрерывно-дифференцируемы на
- непрерывно-дифференцируемы на 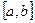 , то
, то 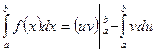 .
.
Все замечания, сделанные к аналогичному методу в неопределенном интеграле остаются справедливыми.- Определенный интеграл на отрезке симметричном нулю от нечетной функции равен нулю, от четной – двум интегралам, взятым по половине исходного отрезка интегрирования:
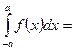
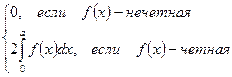 .
.
12.3. Несобственные интегралы:
Первого рода:
Пусть  - непрерывна на
- непрерывна на 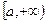 или на
или на 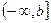 : 1.
: 1. 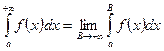 или
или 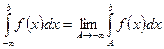 ,
,
если эти пределы существуют и конечны, то соответствующий несобственный интеграл называется сходящимся, если не существует или равен бесконечности, то расходящимся.
2. 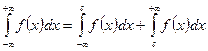 , где
, где 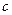 - любая точка оси
- любая точка оси 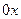 .
.
Полный интеграл 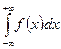 сходится, тогда и только тогда, когда сходится каждый из составляющих его интегралов.
сходится, тогда и только тогда, когда сходится каждый из составляющих его интегралов.
Второго рода:
Пусть  - непрерывна в
- непрерывна в 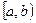 или
или 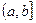 :
:
1. 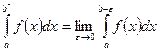 или
или 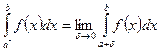 ,
,
если эти пределы существуют и конечны, то соответствующий несобственный интеграл называется сходящимся, если не существует или равен бесконечности, то расходящимся.
2. 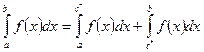 , где
, где 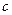 - внутренняя точка бесконечного разрыва.
- внутренняя точка бесконечного разрыва.
Такой несобственные интеграл, сходится тогда и только тогда, когда сходятся оба составляющих его интеграла.
12.4 Применения определенного интеграла:
1. Вычисление площадей плоских фигур:
· 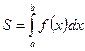 - площадь криволинейной трапеции, где
- площадь криволинейной трапеции, где 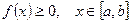 ;
;
· 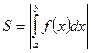 - площадь криволинейной трапеции, где
- площадь криволинейной трапеции, где 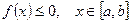 ;
;
· 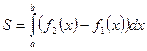 - площадь фигуры, где
- площадь фигуры, где 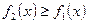 ,
, 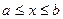 ;
;
· 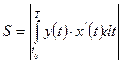 -площадь фигуры, где основная кривая задана как
-площадь фигуры, где основная кривая задана как 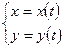 ,
,
где 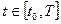 ,
, 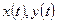 - непрерывно-дифференцируемы на
- непрерывно-дифференцируемы на 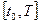 ;
;
· 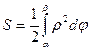 - площадь фигуры, где основная кривая задана в п.с.к. уравнением
- площадь фигуры, где основная кривая задана в п.с.к. уравнением 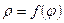 ,
, 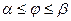 .
.
2.Вычисление длин дуг плоских кривых:
· 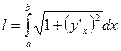 - формула вычисления длины дуги, заданной явно
- формула вычисления длины дуги, заданной явно 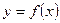 , где
, где  - непрерывно-дифференцируема на
- непрерывно-дифференцируема на 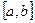
· 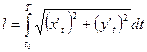 - для дуги, заданной параметрически
- для дуги, заданной параметрически 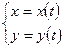 , где
, где 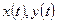 - непрерывно-дифференцируемы на
- непрерывно-дифференцируемы на 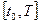 .
.
· 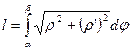 - для дуги кривой в п.с.к., где
- для дуги кривой в п.с.к., где 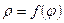 и
и 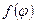 - непрерывно-дифференцируема на
- непрерывно-дифференцируема на 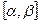 .
.
3. Вычисление площадей поверхностей вращения:
· 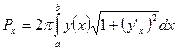 - вокруг оси
- вокруг оси 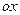 ;
;
· 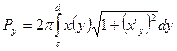 - вокруг оси
- вокруг оси 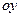 ;
;
· 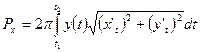 - для кривой, заданной параметрически;
- для кривой, заданной параметрически;
· 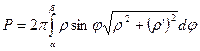 - для кривой в п.с.к.
- для кривой в п.с.к.
4. Вычисление объемов тел вращения:
· 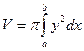 - вокруг оси
- вокруг оси 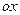 ;
;
· 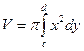 - вокруг оси
- вокруг оси 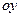 .
.
5. Физические приложения определенного интеграла:
· 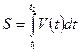 -формула нахождения пути по скорости при прямолинейном движении;
-формула нахождения пути по скорости при прямолинейном движении;
· 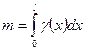 - масса неоднородного стержня длины
- масса неоднородного стержня длины 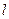 с заданной линейной плотностью
с заданной линейной плотностью 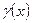 ;
;
· 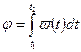 - угол поворота за отрезок времени
- угол поворота за отрезок времени 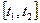 при заданной угловой скорости
при заданной угловой скорости 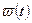 ;
;
· 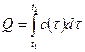 - количество теплоты необходимое для нагревания тела от
- количество теплоты необходимое для нагревания тела от 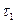 до
до 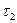 при заданной теплоемкости
при заданной теплоемкости 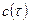 ;
;
· 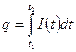 - количество электричества, протекающего через поперечное сечение проводника за отрезок времени
- количество электричества, протекающего через поперечное сечение проводника за отрезок времени 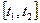 при заданной силе тока
при заданной силе тока 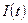 ;
;
· 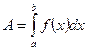 - работа переменной силы при прямолинейном перемещении (физический смысл определенного интеграла);
- работа переменной силы при прямолинейном перемещении (физический смысл определенного интеграла);
· 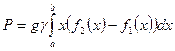 - формула вычисления давления жидкости на вертикальную пластину.
- формула вычисления давления жидкости на вертикальную пластину.
 2015-06-26
2015-06-26 3475
3475
