14.1. Определение и свойства двойного интеграла:
Пусть 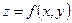 непрерывна в замкнутой области
непрерывна в замкнутой области 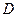 .
.
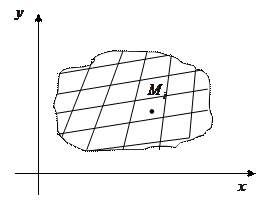
Определение: Конечный предел интегральной суммы функции 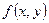 в области
в области 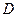 при условии, что
при условии, что 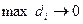 и
и 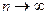 называется двойным интегралом от этой функции по области
называется двойным интегралом от этой функции по области 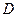 , где
, где 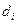 - диаметр частичной области.
- диаметр частичной области.
Т.о. 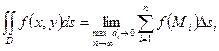 .
.
Основные свойства двойного интеграла:
1) 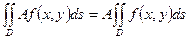 , где
, где  -
- 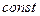 ;
;
2) 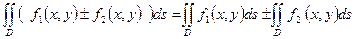 ;
;
3) 
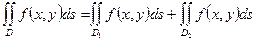 ;
;
4)  Если всюду в области
Если всюду в области 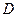
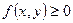 , то
, то 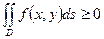 ;
;
5) Если всюду в области 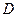
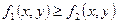 , то
, то 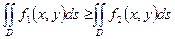 ;
;
6) Если 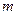 - наименьшее,
- наименьшее, 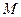 - наибольшее значения функции
- наибольшее значения функции 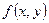 и области
и области 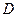 , то
, то 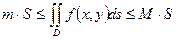 , где
, где 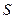 - площадь области
- площадь области 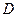 ;
;
7) 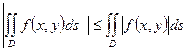 ;
;
8) Теорема о среднем:
Если функция 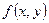 - непрерывна в замкнутой области
- непрерывна в замкнутой области 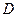 , то
, то 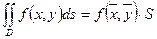 , где
, где 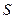 - площадь области
- площадь области 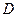 и
и 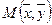 - некоторая внутренняя точка области
- некоторая внутренняя точка области 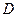 .
.
Двойной интеграл от неотрицательной функции определяет объем соответствующего цилиндрического тела.
14.2. Вычисление двойного интеграла:
1. 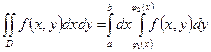
Правило вычисления двойного интеграла по 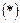 :
:
- строим область интегрирования 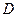 и проверяем, является ли она правильной и стандартной по
и проверяем, является ли она правильной и стандартной по 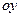 ;
;
- разрешаем уравнение границ области относительно 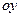 ;
;
- переходим от двойного интеграла к повторному;
- берем внутренний интеграл по 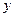 при произвольном постоянном
при произвольном постоянном  ;
;
- вычисляем внешний интеграл.
2. 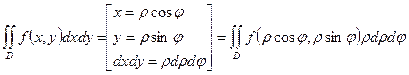 .
.
14.3. Применения двойного интеграла:
· 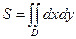 или
или 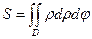 - вычисление площади фигур;
- вычисление площади фигур;
· 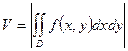 - вычисление объема;
- вычисление объема;
· 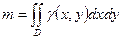 - масса плоской неоднородной пластины плотности
- масса плоской неоднородной пластины плотности 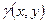 (механический смысл двойного интеграла);
(механический смысл двойного интеграла);
· 4) 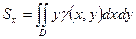 ;
; 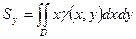 - статические моменты относительно осей
- статические моменты относительно осей
· 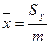 ;
; 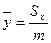 - координаты центра масс пластины;
- координаты центра масс пластины;
· 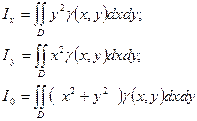 - моменты инерции пластины.
- моменты инерции пластины.
14.4. Определение и вычисление тройного интеграла:
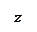 Пусть функция
Пусть функция 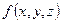 непрерывна в замкнутой облости
непрерывна в замкнутой облости 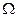 .
.
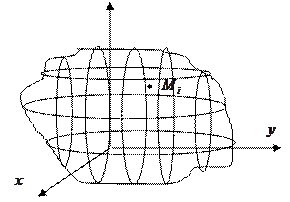 Определение: Конечный предел интегральной суммы функции
Определение: Конечный предел интегральной суммы функции 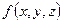 в области
в области 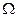 при условии, что
при условии, что 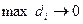 и
и 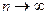 называется тройным интегралом от этой функции по области
называется тройным интегралом от этой функции по области 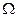 , где
, где 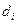 - диаметр частичной области.
- диаметр частичной области.
Т.о. 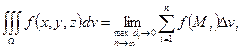 .
.
Вычисление тройных интегралов:
1.В декартовой системе координат:
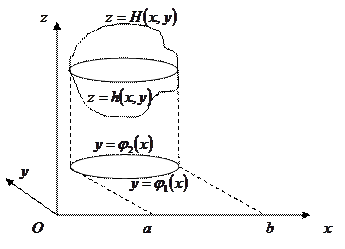
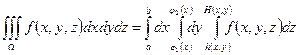
2. В цилиндрической системе координат (ц.с.к.):
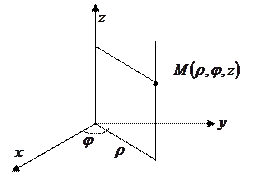 В ц.с.к.
В ц.с.к.
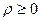 ,
,
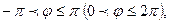
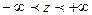 .
.
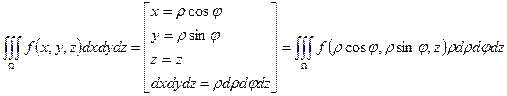 ;
;
Полезно использовать, что 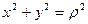 .
.
Тройной интеграл целесообразно вычислять в ц.с.к., если:
- область интегрирования 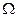 ограничена хотя бы одной из поверхностей
ограничена хотя бы одной из поверхностей 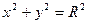 (прямой круговой цилиндр),
(прямой круговой цилиндр), 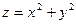 (параболоид вращения),
(параболоид вращения), 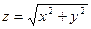 (прямой круговой конус) с
(прямой круговой конус) с 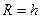 ;
;
- область 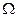 проецируется на плоскость
проецируется на плоскость 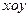 в круг или любую его часть.
в круг или любую его часть.
3. В сферической системе координат (с.с.к.):
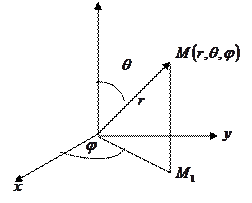
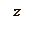

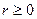 ;
;
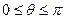 ;
;
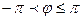 .
.
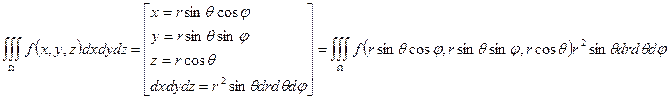 Тройной целесообразно вычислять в с.с.к., если
Тройной целесообразно вычислять в с.с.к., если 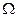 - шар или его часть.
- шар или его часть.
Полезно использовать, что 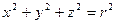 .
.
14.5. Применения тройного интеграла:
· 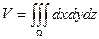 - в декартовой системе координат;
- в декартовой системе координат;
· 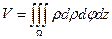 - в цилиндрической системе координат;
- в цилиндрической системе координат;
· 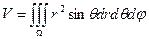 - в сферической системе координат;
- в сферической системе координат;
· 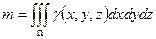 - масса неоднородного тела
- масса неоднородного тела 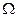 с плотностью
с плотностью 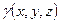 ;
;
· 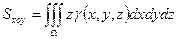 ;
;
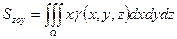 ;
;
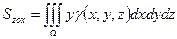 - статические моменты относительно координатных плоскостей.
- статические моменты относительно координатных плоскостей.
· 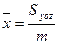 ;
; 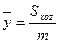 ;
; 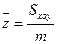 - координаты центра масс;
- координаты центра масс;
· 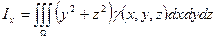 ;
;
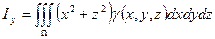 ; - моменты инерции тела относительно коорд. осей
; - моменты инерции тела относительно коорд. осей
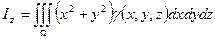 ;
; 
· 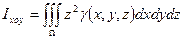 ;
;
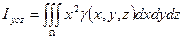 ; - моменты инерции тела относительно коорд. плоскостей
; - моменты инерции тела относительно коорд. плоскостей
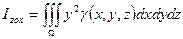
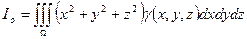 - момент инерции относительно
- момент инерции относительно 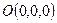 .
.
 2015-06-26
2015-06-26 2482
2482








