Эффективное сечение и длина свободного пробега

1.1. Эффективное сечение.

Молекулы газа не все время движутся свободно, а сталкиваются с другими молекулами, в результате чего изменяют направление движения. Столкновения могут приводить и к другим последствиям, например, ионизация, реакция, возбуждение и девозбуждение и т.д.

Для описания вероятности столкновения с определенным результатом вводится эффективное сечение s.

Будем считать падающую частицу точечной, а частицу мишени имеющей такие размеры, что максимальная площадь, перпендикулярная направлению падающей частицы, равной s. Это воображаемая площадь, а не геометрическая. Она подбирается такой, чтобы вероятность рассматриваемого результата столкновения была равна вероятности того, что падающая частица, двигаясь прямолинейно без взаимодействия с другими частицами, попадет в площадку s.

Ранее в курсе механики мы вводили понятие эффективного дифференциального сечения

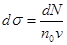(1.1)

как отношения числа частиц 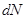, рассеянных в углы от 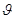до 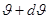, к плотности потока 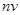падающих частиц (интенсивности пучка). Так, для дифференциального сечения рассеяния на твердом шаре получали:

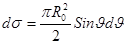, (1.2)

а полное сечение рассеяния (выбывания частицы из начального пучка) равнялось:

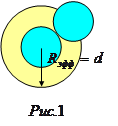
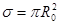, (1.3)

где 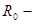радиус твердого шара.

В нашем случае молекулы газа также имеют размеры, которые можно

задать введением некоторого параметра. Введем понятие эффективного

диаметра молекулы по аналогии с радиусом эффективного твердого шара

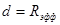, на котором рассеивается молекула, рассматриваемая как

материальная точка.

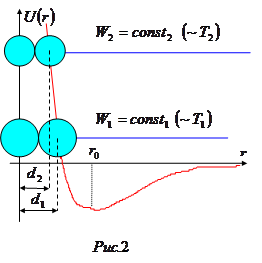
Как видно из рисунка 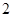, эффективный диаметр молекулы 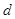уменьшается с ростом температуры, но это изменение сравнительно мало. Поэтому можно записать эффективное сечение рассеяния молекул аналогично рассеянию на твердом шаре:

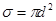(1.4)

Поскольку в объеме, в котором движется молекула

содержится не одна, а много других молекул газа, то

надо определить вероятность столкновения

рассматриваемой молекулы с одной из молекул,

оказывающихся на пути её движения.

Пусть концентрация молекул мишени равна .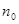

Тогда на пути 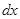в объеме с поперечным сечением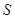

содержится 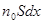молекул мишени.

В этом случае суммарное сечение рассеяния равно

.

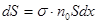Поэтому вероятность того, что частица попадет

в одну из молекул мишени, т.е. рассеется

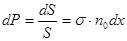. (1.5)

1.2. Длина свободного пробега. Распределение по длинам свободного пробега.

Длина свободного пробега – это путь, который проходит молекула за время между двумя последовательными столкновениями.

Используя выражение (1.5), можно провести сравнительно простое рассуждение, позволяющее определить среднюю длину свободного пробега молекулы.

Эффективное сечение 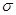и концентрация частиц 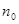не зависят от координаты 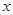, поэтому вероятность столкновения растет пропорционально 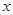. Длина пути, на которой вероятность столкновения рассматриваемой молекулы с другими молекулами газа 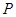равна единице, и есть средняя длина свободного пробега

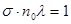, (1.6)

откуда имеем для средней длины свободного пробега, обозначаемой :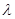

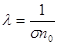. (1.7)

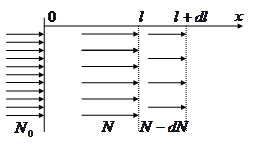Поскольку каждая молекула движется хаотически, а все молекулы газа статистически распределены по объему, то иногда молекуле между двумя последовательными соударениями удается преодолеть довольно большое расстояние, в других случаях это расстояние может быть весьма малым. Т.о., длина свободного пробега является случайной величиной и должна подчиняться статистическим закономерностям.

Найдем распределение по длинам свободного пробега и среднюю длину свободного пробега молекулы,

используя методы статистической физики.

Определим число частиц в пучке, которые испытали

столкновение с молекулами мишени на промежутке от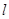

до .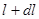

Пусть число частиц, которые пролетели расстояние 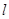без

столкновения равно 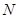, а расстояние .

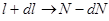Тогда относительное число частиц, «выбывших» из пучка,

равно

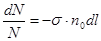(1.8)

Знак “минус” в формуле (1.8) показывает, что число частиц в пучке убывает с ростом .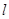

Обозначим

.

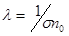Тогда

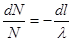
Интегрируем (1.8) с учетом того, что число падающих на мишень частиц (при 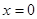) равно .

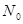Получаем

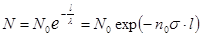(1.9)

Формула (1.9) определяет число молекул 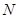, проходящих путь 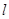без столкновений. Тогда вероятность молекуле пройти путь 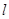, не испытав столкновений, равна

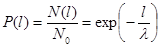(1.10)

Чтобы получить функцию распределения 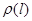запишем вероятность того, что частица испытает столкновение на участке от 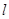до :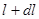

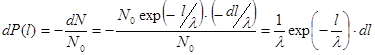
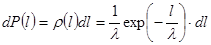(1.11)

Итак, плотность вероятности

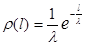(1.12)

Условие нормировки записывается в виде:

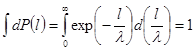(1.13)

Найдем среднюю длину свободного пробега.

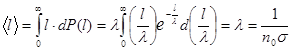
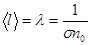(1.14)

Но этот результат справедлив в предположении, что все молекулы мишени неподвижны.

1.3. Учет движения молекул мишени.

Движение рассеиваемой молекулы можно представить как полет внутри некого туннеля – коленчатого цилиндра.

Объем коленчатого цилиндра (при 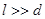) равен

.

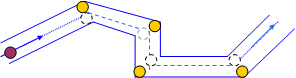
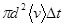Число столкновений, которые испытает

интересующая нас молекула, равно числу молекул

мишени, попавших в объем такого цилиндра:

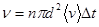, (1.15)

где 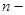концентрация молекул газа.

Если бы все молекулы в объеме были неподвижны, то под средней скоростью 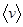следовало бы понимать среднюю скорость налетающей частицы. Однако все молекулы газа находятся в непрерывном движении, поэтому среднюю скорость 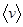следует рассматривать как среднюю скорость движения молекул относительно друг друга, т.е. 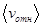. По определению относительная скорость равна:

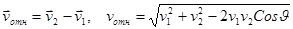(1.16)

где 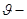угол между векторами скоросте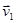й и 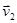(налетающей молекулы и молекулы-мишени).

Чтобы найти среднее значение относительной скорости 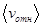, можно использовать распределение Максвелла по скоростям. Однако при этом придется производить довольно сложные вычисления, поэтому мы воспользуемся более простым приемом.

.

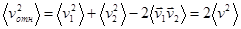Поскольку 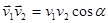и все значения угла 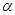равновероятны (скорости сталкивающихся молекул могут быть с одинаковой вероятностью направлены под любым углом друг к другу), то .

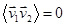Далее, используя тот факт, что 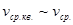, получим

.

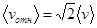Тогда число соударений, определяемое средней скоростью относительного движения молекул, за время 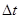будет равно

.

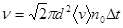Средняя длина свободного пробега 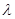может быть представлена как отношение пути, пройденного молекулой за время 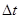к числу столкновений с молекулами газа за тот же промежуток времени.

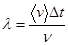. (1.17)

Отсюда средняя длина свободного пробега молекулы:

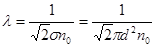
Примечание:

1). Если температура постоянна 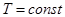, то средняя длина свободного пробега 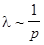, т.к. плотность

.

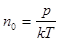2). При нормальных условиях 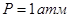, , 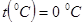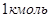газа занимает объем 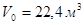. Отсюда 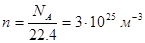. Диаметр молекулы составляет примерно 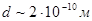. Тогда длина свободного пробега и частота столкновений равны, соответственно

; .

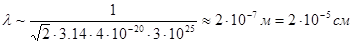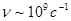2.1. Средняя длина свободного пробега в одном направлении.

Рассмотрим теперь одномерную задачу, т.е. нас будет интересовать пробег, совершаемый молекулой вдоль выделенного направления. Такой упрощенный подход правомерен, поскольку он охватывает все существенные черты изучаемых явлений.

Рассмотрим объем 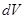, испытав последнее столкновение в котором, молекулы могут достичь площадки .

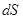Пусть объем 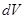содержит 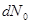молекул, испытавших в нем столкновение

.

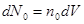Доля молекул, летящих после столкновения к площадке 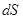, равна отношению телесного угла, под которым видна эта площадка из объема 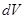к полному телесному углу:

.

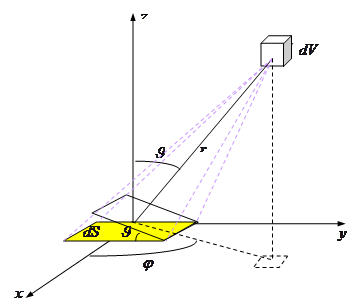
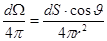Далее, доля молекул, долетевших до площадки

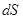без столкновения, определяется множителем

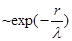(см. (1.9)).

Тогда полное число молекул, не испытавших

на пути из элементарного объема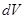

столкновений и пересекших площадку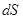

определяется как

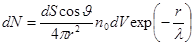(2.1)

Можно записать вероятность 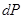молекуле

долететь из объема 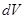до площадки 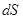без

столкновений с другими молекулами, выразив

объем 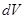в сферических координатах и введя

нормировочную постоянную :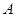

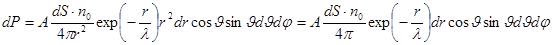. (2.2)

Тогда среднее расстояние по оси 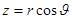определяется стандартным образом (делим на нормировочный интеграл):

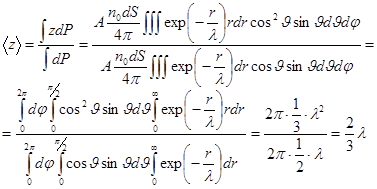. (2.3)

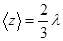. (2.4)

Т.о., мы нашли, что среднее расстояние, пролетаемое молекулой в направлении оси 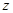после последнего столкновения до пересечения площадки 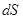, составляет 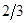от среднего значения длины свободного пробега.