Теплопроводностью называется один из способов переноса теплоты от более нагретых частей системы к менее нагретым. Теплопроводность возникает, когда по каким-либо внешним причинам в газе возникает градиент температуры, т.е. когда в разных точках пространства средние кинетические энергии молекул газа оказываются различными. Перенос энергии при теплопроводности осуществляется в результате непосредственной передачи энергии при столкновениях от частиц, обладающих большей энергией, частицам с меньшей энергией. Если относительное изменение температуры 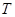 на расстоянии длины свободного пробега частиц
на расстоянии длины свободного пробега частиц 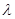 мало, то выполняется основной закон теплопроводности – закон Фурье.
мало, то выполняется основной закон теплопроводности – закон Фурье.
3.1. Уравнение Фурье.
Рассмотрим газовую среду, в которой значение температуры зависит от координаты 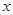 , так что
, так что 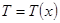 . Т.о., газ находится в неравновесном состоянии, и стремление системы к равновесному состоянию проявится в появлении потока тепла, направленного от участков, обладающих высокой температурой, к участкам с более низкой температурой.
. Т.о., газ находится в неравновесном состоянии, и стремление системы к равновесному состоянию проявится в появлении потока тепла, направленного от участков, обладающих высокой температурой, к участкам с более низкой температурой.
Итак, переносимым молекулами качеством в рассматриваемом случае является тепло (кинетическая энергия), следовательно, в уравнении стационарных процессов переноса 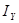 приобретает смысл плотности потока тепла
приобретает смысл плотности потока тепла 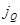 в направлении оси
в направлении оси 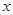 . В этом случае
. В этом случае 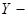 средняя энергия теплового движения, приходящаяся на одну молекулу. Она изменяется вместе с изменением температуры среды.
средняя энергия теплового движения, приходящаяся на одну молекулу. Она изменяется вместе с изменением температуры среды.
Исходя из теоремы о равнораспределении энергии по степеням свободы (здесь и далее температуру измеряем в градусах Кельвина 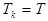 ), можем записать
), можем записать
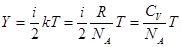 . (3.1)
. (3.1)
Тогда
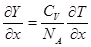 (3.2)
(3.2)
и
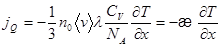 . (3.3)
. (3.3)
Введенный в последнем выражении коэффициент 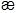 называется коэффициентом теплопроводности:
называется коэффициентом теплопроводности:
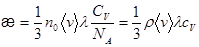 (3.4)
(3.4)
где 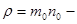 плотность газа (
плотность газа (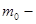 масса молекулы),
масса молекулы), 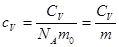 - удельная теплоемкость.
- удельная теплоемкость.
Итак, уравнение Фурье (стационарное уравнение теплопроводности) имеет вид:
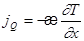 (3.5)
(3.5)
 |
1. Коэффициент теплопроводности не зависит от давления. Появление зависимости говорит о появлении вакуума (длина свободного пробега молекул становится сравнимой с размерами сосуда). Из рисунка видно, когда можно ввести понятие вакуума.
2. Коэффициент теплопроводности зависит от температуры как 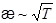 , т.к.
, т.к.
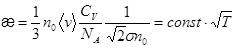 , (3.6)
, (3.6)
т.е. зависимость 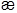 от температуры определяется присутствием в выражении (3.6) средней скорости молекул, поскольку эффективное сечение
от температуры определяется присутствием в выражении (3.6) средней скорости молекул, поскольку эффективное сечение 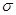 слабо зависит от температуры.
слабо зависит от температуры.
3. Размерность 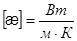 .
.
4. Полное количество тепла, переносимое через поверхность 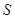 , определяется интегралом по поверхности:
, определяется интегралом по поверхности:
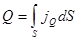 . (3.7)
. (3.7)
3.2. Нестационарное уравнение теплопроводности.
В результате переноса тепла температуры тел (если они какими-либо средствами не поддерживаются постоянными) со временем выравниваются, что приводит к изменению со временем градиента температуры, вследствие чего и поток тепла будет зависеть от времени: 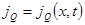 .
.
Найдем уравнение теплопроводности, зависящее от времени, т.е. учтем изменение температуры при переносе тепла.
Рассмотрим поток тепла через поперечное сечение цилиндра 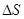 . Количество тепла, приходящее за время
. Количество тепла, приходящее за время 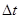 к поверхности
к поверхности 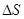 с координатой
с координатой 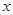 , равно
, равно
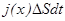 .
.
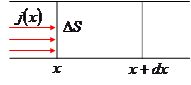 Тепло, уходящее через поверхность
Тепло, уходящее через поверхность 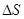 , имеющую координату
, имеющую координату
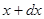 :
:
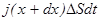 .
.
Тогда изменение количества тепла на промежутке 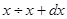
можно определить как
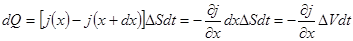 . (3.8)
. (3.8)
С другой стороны, изменение количества тепла в объеме 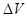 равно
равно
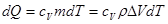 , (3.9)
, (3.9)
где 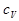 - удельная теплоемкость,
- удельная теплоемкость, 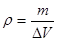 - плотность газа.
- плотность газа.
Сравнивая (3.8) и (3.9), находим
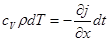 (3.10)
(3.10)
и приходим к уравнению:
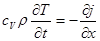 . (3.11)
. (3.11)
Здесь 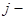 плотность потока тепла через выбранную поверхность, т.е. величина, определяемая уравнением Фурье (3.5).
плотность потока тепла через выбранную поверхность, т.е. величина, определяемая уравнением Фурье (3.5).
Подставляя выражение для 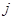 из (3.5) в (3.11), получаем уравнение теплопроводности (нестационарное):
из (3.5) в (3.11), получаем уравнение теплопроводности (нестационарное):
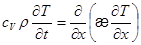 . (3.12)
. (3.12)
Частный случай: среда однородна и коэффициент теплопроводности не зависит от температуры (такое может быть, если процесс протекает не в газе):
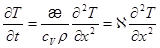
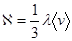 (3.13)
(3.13)
Для решения нестационарного уравнения теплопроводности (3.12) необходимо знать начальные и граничные условия.
Если известно, что существуют источники тепла (ток, распад), то их присутствие можно учесть, если ввести мощность источников – количество тепла, выделяемое в 1 объема в 1 времени.
Тогда искомое уравнение примет вид:
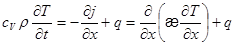 (3.14)
(3.14)
3.3. Распределение температуры между двумя концентрическими сферами.
В качестве примера рассмотрим стационарное распределение температуры между двумя концентрическими сферами, при температуры которых поддерживаются равными 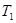 и
и 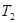 . т.е.
. т.е. 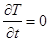 .
.
Тогда из (3.11) имеем 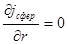 , где
, где 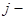 поток тепла через сферическую поверхность.
поток тепла через сферическую поверхность.
Таким образом, поток тепла через любую сферу постоянен
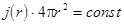 (3.15)
(3.15)
Подставляя сюда поток тепла из уравнения Фурье, имеем:
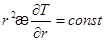 (3.16)
(3.16)
а). Если коэффициент 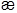 постоянен, то
постоянен, то 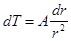 и, интегрируя, получаем
и, интегрируя, получаем
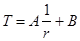 . (3.17)
. (3.17)
Коэффициенты 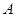 и
и 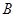 находятся из граничных условий (при
находятся из граничных условий (при 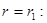
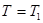 , при
, при 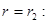
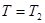 ).
).
Т.о., распределение температуры имеет вид:
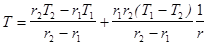 . (3.18)
. (3.18)
б). Если 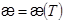 , то
, то 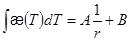 и снова находим
и снова находим 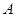 и
и 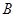 из граничных условий.
из граничных условий.
 2015-06-26
2015-06-26 1576
1576
