Классификация движений второго рода

Из формул (2)

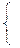
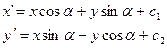
при условии, что х = х¢, y = y¢ получаем следующие уравнения для нахождения координат неподвижных точек движения второго рода:

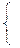
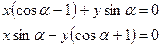
Определитель этой системы при любом a равен нулю, и не все коэффициенты при х и у равны нулю, поэтому любое движение второго рода либо имеет прямую инвариантных точек, либо не имеет ни одной инвариантной точки. Рассмотрим каждый из этих случаев в отдельности.

1) Движение g - имеет прямую инвариантных точек. Пусть h - какой-нибудь луч этой прямой. Т.к. h = g(h), то по лемме 2 g - либо тождественное преобразование, либо осевая симметрия. Но тождественное преобразование является движением первого рода, поэтому g - осевая симметрия.

2 ) Движение g не имеет инвариантных точек.

Выберем ортонормированный репер (О, Е₁, Е₂) так, чтобы точки О и Е₁ лежали на инвариантной прямой ℓ. Пусть О₁ = g(О), О₂ = g(О₁). Если точка О₁ имеет координаты (а, о), то О₂ имеет координаты (2а, 0). Предположим, что аналитическое выражение движения g в репере (О, Е₁, Е₂) имеет вид (2).

Из условий О® О₁, О₁® О₂ получаем

с₁ = а, с₂ = 0, cosa = 1, sina = 0.

Поэтому:

х' = х + а,

у' = –у. (3)

Следовательно, мы имеем формулы скользящей симметрии относительно прямой ℓ. При этом, g = sf, где f – параллельный перенос на ненулевой вектор 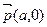, а s – симметрия от прямой ℓ. В самом деле, преобразование S и f в репере (О, Е₁, Е₂) определяются по формулам:

s: 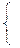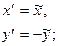f: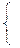

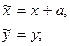
поэтому отображение sf определяется формулами (3), т.е. совпадают с g. Ясно, что скользящая симметрия не имеет инвариантных точек и имеет только одну инвариантную прямую.

Итак, существуют четыре типа движений, которые представим в виде таблицы.

Название движения	Инвариант-ные точки	Инвариантные прямые
I. Движение первого рода
1. Поворот на угол a а) Поворот на угол a¹0 и a ¹ ±p	Центр поворота	Нет
б)тождественное преобразование (a = 0)	Любая точка плоскости	Любая прямая плоскости
в)центральная симметрия (a = ±p)	Центр симметрии	Любая прямая, проходящая через центр симметрии
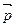2. Параллельный перенос на вектор а)параллельный перенос на вектор 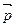¹ 0	Нет	Любая прямая, параллельная вектору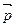
б)тождественное преобразование (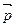 = 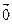)	Любая точка плоскости	Любая прямая плоскости
II. Движение второго рода.
3. Осевая симметрия	Все точки оси	Ось симметрии и любая прямая, перпендикулярная к ней.
4.Скользящая симметрия	Нет	Одна прямая