 Теорема 4. При любом движении плоскости ортонормированный репер отображается в ортонормированный репер.
Теорема 4. При любом движении плоскости ортонормированный репер отображается в ортонормированный репер.
Доказательство. В самом деле, пусть (А, В, С) данный репер, а А', В',С' - образы соответственно точек А, В и С. Т.к. точки А, В и С не лежат на одной прямой, то
|АВ|< |АС| + |СВ|, |ВС| < |ВA| + |АС|, |СА| < |СВ| + |ВА|.
Движение сохраняет расстояния, поэтому
|А'В'|<|А'С'|+|С'В'|, |В'С'| < |В'А'|+|А'С'|, |С'А'| < |С'В'|+|В'А'|.
Следовательно, точки А',В',С ' не лежат на одной прямой.
Таким образом, получили, что (А',В',С') - репер.
Если (А,В,С) - ортонормированный репер, то по теореме Пифагора
|АВ|2 + |АС|2 = |ВС|2,
Поэтому
|А'В'|2+ |А'С'|2= |В'С'|2.
По теореме, обратной теореме Пифагора,  А'В'С ' - прямоугольный.
А'В'С ' - прямоугольный.
Учитывая, что
|А'В'| = |АВ| = 1, |А'С'| = |АС| =1,
получим: (А',В',С') - ортонормированный репер.
Теорема доказана.. ▄
Теорема 5. Пусть R = (А,В,С) и R' = (А',В',С') – произвольные ортонормированные реперы плоскости s. Тогда существует одно и только одно движение, которое репер R переводит в репер R'. При этом движении любая точка М с данными координатами (х, у) в репере R переходит в точку М' с теми же координатами (х, у) в репере R '.
Доказательство. 1. Докажем сначала, что существует движение, которое репер R переводит в репер R'.
Построим отображение g: s®s следующим образом. Произвольной точке М с координатами (х, у) в репере R поставим в соответствие точку М' с теми же координатами в репере R '.
Тогда
g: А(0,0)R ® А'(0,0)R', В(0,1)R ® В'(1,0)R' и С(0,1)R ® А' 0,1)R'.
Очевидно, отображение g: s ® s является преобразованием плоскости s.
Докажем, что отображение g сохраняет расстояния. Пусть М1 и М2 - произвольные точки плоскости, которые в репере R имеют координаты М1(х1, у1)R и М2(х2, у2)R.
Тогда
|М1М2| = 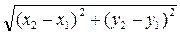 .
.
Образы М1' и М2 ' точек М1 и М2 в репере R' имеют те же координаты:
М1'(x1,y1)R', М2'(x2,y2)R',
Поэтому
|М1'М2'| = 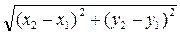
и
|М1М2| = |М1'М2'|.
Т.о. преобразование g -искомое движение, которое переводит репер R в репер R '.
2) Докажем, что g - единственное движение, которое переводит репер R в репер R '.
Допустим, что это не так, т.е. существует другое движение ¦, такое, что R'= ¦(R). Тогда на плоскости существует такая точка М, что образ М1 этой точки при движении g не совпадает с образом М2 той же точки при движении ¦.
Т.к. 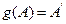 и
и 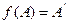
то
|АМ| = |А'М1|, |АМ| = |А'М2|.
Поэтому
|А'М1| = |А'М2|,
т.е. точка А' равноудалена от концов отрезка М1М2. Аналогично, точки В', С' равноудалены от концов отрезка М1М2. Т.о. точки А', В', С' лежат на серединном перпендикуляре отрезка М1М2, т.е. на одной прямой, что противоречит определению репера.
Итак, 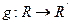 ' и
' и 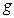 - единственное движение. При этом движении М(х,у)R переходит в М'(х,у)R'.
- единственное движение. При этом движении М(х,у)R переходит в М'(х,у)R'.
. ▄
Используя эту теорему, легко доказать следующие свойства движения:
10. Движение переводит прямую в прямую, а параллельные прямые - в параллельные прямые.
20. Движение переводит полуплоскости с границей а в полуплоскость с границей а ¢, где а ¢ - образ прямой а.
30. Движение сохраняет простое отношение трех точек прямой.
40. Движение сохраняет отношение “лежать между”.
50. Движение переводит отрезок АВ в отрезок А¢В¢, где А¢ и В¢ - образы точек А и В. При этом середина отрезка АВ переходит в середину отрезка А¢В ¢.
60. Движение переводит луч в луч.
70. Движение переводит угол в равный ему угол.
80. Движение переводит взаимно перпендикулярные прямые во взаимно перпендикулярные прямые.
 Вывод формул движения.
Вывод формул движения.
Пусть реперы R = (O 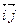 ) и R
) и R  = (O
= (O 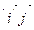 ) определяют движение g. При этом точка M в старом репере R имеет координаты (х, у), а в новом репере R¢ ее образ, точка М¢, имеет те же координаты (х, у) и координаты (х¢, у¢) относительно репера R = (O
) определяют движение g. При этом точка M в старом репере R имеет координаты (х, у), а в новом репере R¢ ее образ, точка М¢, имеет те же координаты (х, у) и координаты (х¢, у¢) относительно репера R = (O 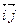 ). Репер R¢ = (O
). Репер R¢ = (O 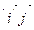 ) задается относительно репера R = (O
) задается относительно репера R = (O 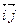 ) как это сделано выше. Наша задача выразить х¢, у¢ через х, у. Для этого достаточно рассмотреть старые и новые координаты точки М¢ и воспользоваться формулами перехода от старой системы координат к новой,
) как это сделано выше. Наша задача выразить х¢, у¢ через х, у. Для этого достаточно рассмотреть старые и новые координаты точки М¢ и воспользоваться формулами перехода от старой системы координат к новой,
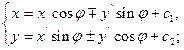
обратив внимание на изменение наличия штрихов в старых и новых координатах.
А. Движение g является движением I рода. Тогда реперы R и R ¢ ориентированы одинаково, поэтому искомые формулы имеют вид:

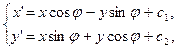 (1)
(1)
Б. Движение g - является движением II рода. Тогда реперы R и R¢ ориентированы противоположно, тогда формулы имеют вид:

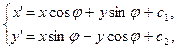 (2)
(2)
Эти формулы можно объединить в одной записи:

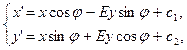 (3)
(3)
где Е = 1, если g – движение I рода, и
Е = –1, если g – движение II рода.
Очевидно, параллельный перенос и поворот плоскости на угол a относятся к движениям I рода
.
 2015-07-04
2015-07-04 3669
3669
