Классификация движений

Определение 1. Точку плоскости назовем инвариантной (неподвижной) точкой преобразования, если она отображается в себя при этом преобразовании.

Определение 2. Прямую назовем инвариантной (неподвижной) прямой преобразования, если любая ее точка переходит в точку этой же прямой.

В частности, прямая является инвариантной, если каждая ее точка инвариантна в данном преобразовании (такую прямую будем называть прямой инвариантных точек). Если, например, g – осевая симметрия, то ось этого преобразования и любая прямая, перпендикулярная к ней, являются инвариантными прямыми, причем ось симметрии – прямая инвариантных точек.

Л е м м а 1. Если движение g не имеет ни одной инвариантной точки. то оно имеет хотя бы одну инвариантную прямую.

Доказательство. Пусть А – произвольная точка плоскости, А₁=g(A), А₂=g(А₁). По условию леммы точка А не совпадает с точкой А₁, а точка А₁ не совпадает с точкой А₂. Если точки А, А₁, А₂ лежат на одной прямой, то эта прямая является инвариантной. Поэтому рассмотрим случай, когда эти точки не лежат на одной прямой. Рассмотрим середины О₁ и О₂ отрезков АА₁ и А₁А₂ и докажем, что О₁О₂ инвариантная прямая. Для этого проведем

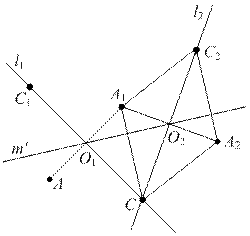
серединные перпендикуляры l ₁ и l ₂ отрезков АА₁ и А₁А₂. Обозначим через С точку их пересечения.

Очевидно, что О₂ равно g(О₁), поэтому l ₂=g(l ₁). Т.к. О₁С=О₂С, то точка С прямой l ₁ переходит либо в ту же точку С прямой l ₂, либо в точку С₂ симметричную точке С относительно О₂. Первый случай не может иметь места, т.к. g не имеет неподвижных точек, поэтому С₂ =g(C). Т.о. прямая А₁С переходит в параллельную ей прямую А₂С₂ (четырехугольник А₁СА₂С₂ - параллелограмм).

Пусть m' - образ прямой (O₁O₂).

Так как (O₁O₂) ^ (A₁C), то m' ^ (A₂C₂) или m' ^ (A₁C).

Мы видим, что прямая m' проходит через точку О₂ и перпендикулярна прямой (A₁C), поэтому m' совпадает с прямой (О₁О₂). Лемма доказана.

▄

Л е м м а 2. Если движение g луч h переводит в себя, то g либо тождественное преобразование, либо отражение от прямой ℓ, содержащей луч h.

Доказательство. Действительно, обозначим через О начало луча h, а через l и l¢ две полуплоскости с общей границей ℓ, содержащей луч h. Выберем прямоугольный декартовый репер R = (ОЕ₁Е₂), где точки О, Е₁ лежат на луче h. Тогда R¢ = (ОЕ₁Е 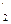) образ репера R для движения g.

Возможны только два случая: точки Е₂ и Е 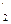лежат в одной полуплоскости l или l¢, или лежат в разных полуплоскостях l и l¢. В первом случае мы получаем тождественное преобразование, так как реперы R и R¢ совпадают. Во втором случае мы получаем движение, которое совпадает с осевой симметрией относительно прямой ℓ. Лемма доказана.

▄

Проведем классификацию движений в зависимости от наличия неподвижных точек и инвариантных прямых.