Скользящая симметрия

Пусть имеем на плоскости прямую d и вектор 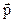|| d.

Определение 12. Преобразование плоскости 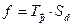называют скользящей симметрией.

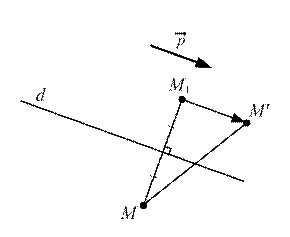
Пусть f: М ® М^' – скользящая симметрия, заданная в прямоугольной декартовой системе координат O .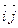

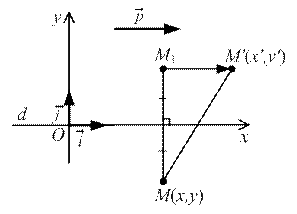
Мы выбрали прямоугольную декартову систему координат O 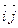так, чтобы прямая d была осью абсцисс. При этом

М(х, у); М₁ (х₁, у₁); М^' (х^', у^').

,

,

,

.

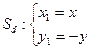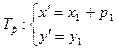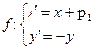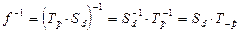Если вектор 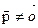, то неподвижных точек нет.

Скользящая симметрия будет обладать свойствами, общими для параллельного переноса и для осевой симметрии, например:

1. Неподвижных точек нет.

2. Неподвижная прямая одна, это прямая d.

3. Всякая прямая, параллельная прямой d имеет образ, параллельный d.

4. Середина О отрезка ММ ^' принадлежит d.

Рассмотренные выше примеры показывают, что множество D всех движений плоскости не пустое. Ясно, что D является подмножеством множества всех преобразований плоскости W, где W есть группа относительно операции умножения.

Теорема 3. Множество D есть группа относительно операции умножения.

Доказательство. Нам достаточно показать, что множество D есть подгруппа относительно группы W.

1. Пусть f₁, f₂ Î D и А, В – произвольные точки плоскости.

Тогда

f₂f₁ (A) = f₂(f₁(A)) = f₂(A¢) = A¢¢,

f₂f₁ (B) = f₂(f₁(B)) = f₂(B¢) = B¢¢.

При этом

|AB| = |A¢B¢|,

|A¢B¢| = |A¢¢B¢¢|,

так как

f₁, f₂ Î D.

Поэтому

|AB|= |A¢¢B¢¢|.

Следовательно,

f₂× f₁ Î D.

2. Пусть f – произвольное движение. Так как f – преобразование плоскости, то для него существует обратное преобразование f ^–1, причем

f ^–1× f = е,

где е – тождественное преобразование плоскости.

Покажем, что преобразование f ^–1 является движением. Действительно. Если

f(A) = A¢, f(B) = B¢,

то

|AB| = |A¢B¢|.

С другой стороны

f ^–1(A¢) = A, f ^–1(B¢) = B.

Так как

|A¢B¢ | = |AB |,

то преобразование f ^–1 является движением.

Теорема доказана. ▄

Определение 13. Две фигуры F и F¢ на плоскости называются конгруэнтными, если они D – эквивалентны, то есть

$fÎD(f(F)=F¢).

В дальнейшее конгруэнтные фигуры будем обозначать:

F @ F¢.

§3. Свойства движений.

Определение 14. Пусть мы имеем три различные точки А, В, С, лежащие на одной прямой. Будем говорить, что точка В лежит между точками А и С, если

|AB| + |BC| = |AC|.

В дальнейшем будем обозначать: (А 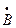С).

Как известно, точки называют коллинерными если они лежат на одной прямой.

Лемма. Для коллинеарности трех точек необходимо и достаточно, чтобы одна из них лежала между двумя другими.

Доказательство. Если точки А, В, С лежат на одной прямой, то, очевидно, возможны следующие случаи взаимного расположения трех точек: (А 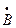С), (В 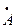С), (С 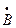А), (С 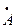В), (А 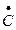В), (В 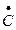А).

С другой стороны, если три точки Х, У, Z не лежат на одной прямой, то выполняется неравенство треугольника:

|XY| + |YZ| > |XZ|,

но тогда точка Y не лежит между точками Х и Z.

. ▄

Свойство 1. Движение плоскости f сохраняет отношение «лежать между» для трех точек прямой.

Действительно. Пусть (А 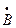С) и f: .

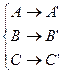Тогда

|AB| + |BC| = |AC|,

|AB| = |A¢B¢|,

|BC| = |B¢C¢|,

|AC| = |A¢C¢|.

Следовательно,

|A¢B¢| + |B¢C¢| = |A¢C¢|

и

(А¢ 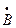¢С¢).

. ▄

Свойство 2. Движение плоскости отображает прямую в прямую, луч в луч, отрезок в отрезок.

Это свойство вытекает непосредственно из предыдущей леммы, свойства 1 и следующего задания отрезка, луча и прямой:

[A, B] = { A, B } È {M| (А 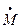B)},

[A, B) = [A, B] È {M| (А 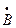M)},

(A, B) = [A, B) È [B, А).

Следствие. Точки, не лежащие на одной прямой, движение отображает в точки, также не лежащие на одной прямой.

Свойство 3. Движение плоскости отображает полуплоскость в полуплоскость.

Доказательство. Пусть прямая (АВ) определяет полуплоскости a и a ¢. Тогда прямая (A¢B¢) = f(AB) разбивает плоскость на две полуплоскости b и b ¢. Наша задача показать, что образы любых двух точек, принадлежащих одной полуплоскости, также принадлежат одной полуплоскости и, наоборот, образы любых двух точек, не принадлежащих одной полуплоскости, также не принадлежат одной полуплоскости.

Пусть точка С Î a ¢, а точка D Îa, тогда [DС]Ç(АВ) =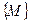

и (D 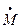С). С другой стороны. Для их образов имеем

(D¢ 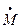¢С¢), где 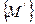= [D¢С¢]Ç(А¢В¢).

Следовательно, точки D¢ и С¢ принадлежат различным полуплоскостям b и b ¢.

Если теперь предположить, что точки С и D принадлежат одной полуплоскости, например a, а их образы С¢ и D ¢ принадлежат различным полуплоскостям, то в силу того, что обратное движение отобразит точки С¢ и D ¢ в точки С и D, принадлежащие разным полуплоскостям, получим противоречие с условием, так как точки С и D принадлежат одной полуплоскости.

. ▄

Свойство 4. Движение плоскости f отображает угол в угол.

Доказательство. Пусть мы имеем угол ÐАОВ. Тогда

f: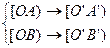

и

f: 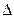AOB 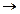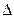A¢O¢B¢.

Поэтому

f: ÐAOB 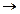ÐA¢O¢B¢.

. ▄

Свойство 5. Движение плоскости сохраняет простое отношение трех точек прямой.

Доказательство. Пусть точка С делит отрезок [AB] в отношении l:

.

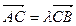С другой стороны имеем

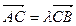Û .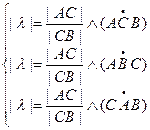

Так как движение сохраняет |l| и отношение «лежать между», то движение сохраняет простое отношение трех точек.

. ▄