Решение

Анализ. Пусть АВСD – квадрат, удовлетворяющий условиям, а именно: вершина А 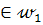, вершина С 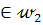, вершины В и D лежат на прямой l

(рис. 1а)

Построим окружность 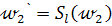. Так как диагональ ВD квадрата является его осью симметрии, то вершина С квадрата отобразится на вершину А. Но вершина С 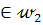, и поэтому вершина А 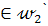. Кроме того вершина А 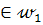. Таким образом, А= 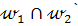, а так как вершина А и ось симметрии l вполне определяют квадрат, то задачу можно свести к построению А=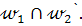

Построение. Строим окружность 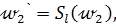находим точку А= 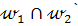, которую отображаем на точку С 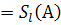. На 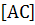как на диаметре строим окружность 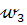и находим точки В= 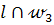и D .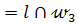

Доказательство. Так как (АС) 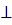l, то при симметрии относительно l прямая АС отображается на себя. Кроме того, окружность 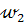симметрична окружности 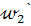. Тогда точка С 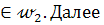, отрезок АС – диаметр окружности 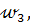точка О=(АС) 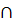l – центр окружности 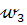, поэтому 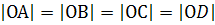. Так как далее 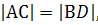(АС) 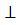(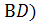, то АВСD – квадрат. Итак, по построению А 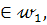В 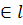, а по доказанному С 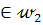, и четырёхугольник АВСD – квадрат.

Таким образом, четырёхугольник АВСD удовлетворяет всем поставленным условиям, т.е. является искомым квадратом.

Исследование. При выбранном способе построения количество решений зависит от количества точек пересечения окружностей 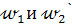и положения этих точек относительно (АС). Возможны следующие случаи:

1) Если окружности 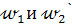пересекаются, то задача либо имеет два решения (рис. 1б), либо имеет одно решение (рис. 1в), либо не имеет решений (рис. 1г);

2) если окружности 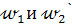касаются, то либо имеется одно решение, либо решений нет;

3) если окружности 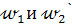не имеют общих точек, то решений нет;

4) если окружности 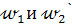совпадают, то решений бесконечное множество.

(Иллюстрации для случаев 2, 3, 4 сделайте самостоятельно.)

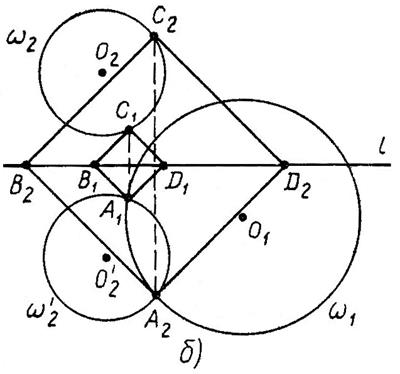
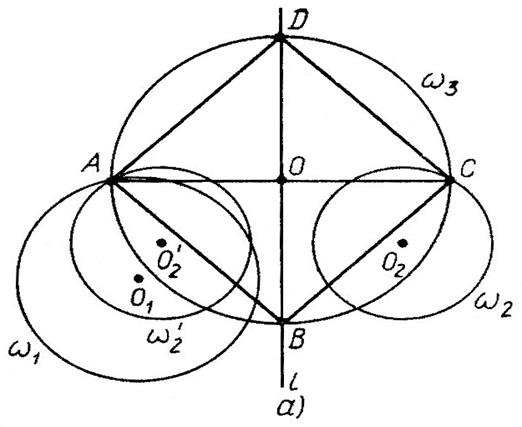
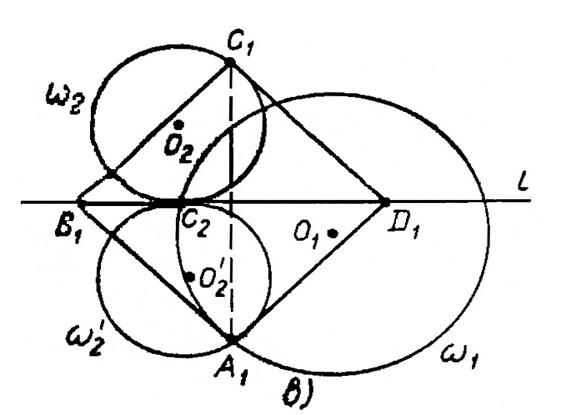
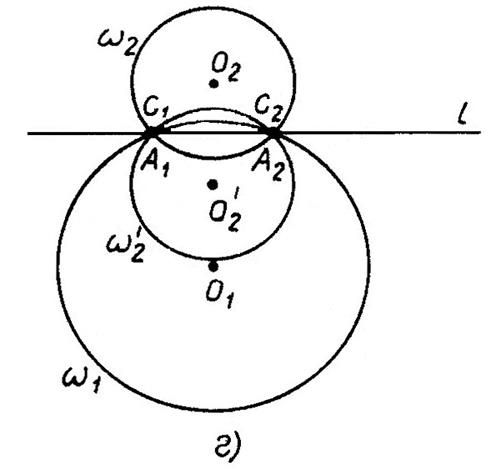
рис.1