Подобие плоскости и его свойства

Определение. Преобразованием подобия плоскостис коэффициентом k (k > 0) называется отображение плоскости в себя, при котором для любых двух точек А, В и их образов А ^¢, В ^¢ выполняется равенство

|А^¢ В^¢ | = k |А В|.

Всякое движение есть преобразование подобия с коэффициентом 1.

Нетрудно видеть, что гомотетия с коэффициентом k есть преобразование подобия с коэффициентом | k |.

Теорема 1. Всякое преобразование подобия можно представить в виде композиции движения и гомотетии.

Доказательство. Пусть 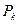– некоторое преобразование подобия с коэффициентом k. Рассмотрим гомотетию 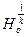с произвольным центром О. Из определения подобия и в силу теоремы 1 § 1 композиция

= ◦

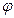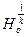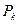
сохраняет расстояние между точками. Следовательно, отображение 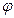есть движение. Из равенства

◦ ◦ = ◦

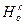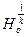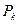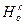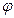
следует

= ◦ .

▄

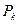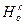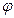Теорема 2. Композиция двух преобразований подобия плоскости есть преобразование подобия.

Доказательство. Пусть мы имеем два подобия плоскости

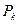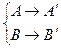: , |А^¢ В^¢ | = k × |А В|,

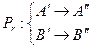, |А¢¢ В¢¢ | = r× |А¢ В¢|.

Так как произведение двух преобразований плоскости есть преобразование плоскости, то из равенства

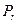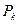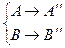◦ : и |А¢¢ В¢¢ | = r× k × |А В|

следует, что композиция подобий 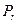◦ 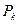есть подобие плоскости с коэффициентом r× k.

▄

Теорема 3. Множество всех преобразований подобия плоскостиесть группа преобразований.

Доказательство. В силу теоремы 2 следует достаточно доказать, что всякое преобразование подобия обратимо и обратное ему преобразование есть преобразование подобия.

Действительно, пусть задано подобие 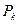. Тогда в силу теоремы 1 имеем разложение его в виде произведения движения на гомотетию

= ◦ .

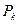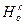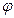Следовательно,

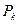()^-1 = ( 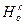◦ 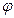)^-1 = j^-1 ◦ (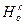)^-1 = j^-1 ◦ .

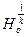Теорема 4. При всяком преобразовании подобия образ прямой есть прямая, образ луча есть луч, образ отрезка есть отрезок. Всякое преобразование подобия сохраняет величину угла.

Доказательство. Действительно любое движение и гомотетия обладает этими свойствами. Поэтому и их композиция сохраняет эти свойства.

▄

Определение. Фигура F называется подобной фигуре F₁ (F ∞ F₁), если существует преобразование подобия, переводящее фигуру F в фигуру F₁.

Теорема 5. Отношение подобия фигур есть отношение эквивалентности.

Доказательство. Чтобы некоторое отношение фигур было отношением эквивалентности, оно должно обладать свойствами рефлексивности, симметричности и транзитивности.

Отношение подобия фигур обладает свойством рефлексивности, так как любая фигура F подобна сама себе. Действительно, тождественное преобразование пространства, являясь подобием, отображает F в F.

Итак, F ∞ F.

Отношение подобия фигур обладает свойством симметричности.

Действительно, если F ∞ F₁, то существует преобразование подобия и имеет место F₁ = 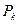(F).

Учитывая свойства подобий, имеем обратное преобразование подобия и при этом F = (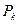)^-1 (F₁). Поэтому F₁ ∞ F.

Следовательно, отношение подобия фигур обладает свойством симметричности.

Отношение подобия фигур обладает свойством транзитивности. Действительно, если

F ∞ F₁,

F₁ ∞ F₂,

то существуют преобразования подобия:

F₁ = 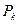(F),

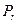F₂ = (F₁).

Так как

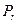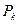◦ (F) = F₂,

То

F ∞ F₂.

Свойство транзитивности доказано.

Теорема доказана.

▄

Подобие треугольников. В школьных учебниках подобие многоугольников определяется через равенство соответствующих углов и пропорциональность соответствующих сторон. Признаки подобия треугольников доказываются на основе этого определения. Докажем один из признаков подобия треугольников, исходя из приведённого здесь более общего определения подобия (оно действительно более общее, поскольку не у всякой фигуры есть стороны и углы).

Теорема 6. Если две стороны одного треугольника пропорциональны двум сторонам другого и углы, заключённые между этими сторонами, равны, то треугольники подобны.

Доказательство. Пусть для треугольников АВС и А^¢B^¢C^¢ выполняются условия

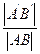= k, 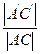= k, ÐA^’ = Ð A.

Применим к треугольнику АВС гомотетию 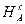. Получим треугольник АВ₁С₁, у которого

|AB₁| = |A^¢B^¢|, |AC₁| = |A^¢C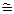^¢|, Ð A ÐA^¢.

Треугольники АВ₁С₁ и А^¢B^¢C^¢ равны. Это значит, что треугольник А^¢B^¢C^¢ есть образ треугольника АВ₁С₁ при некотором движении 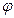. Следовательно, он является образом треугольника АВС при композиции гомотетии 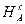и движения 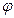, т.е. при преобразовании подобия.

▄

Теорема 7. Если углы одного треугольника соответственно равны углам другого треугольника, то такие треугольники подобны.

Доказательство. Пусть для треугольников АВС и А^¢B^¢C^¢ выполняются условия

Ð A^¢= Ð A, Ð B^¢ = Ð В, ÐС^¢ = Ð С.

Обозначим

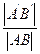= k

и применим к треугольнику АВС гомотетию 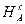. Получим треугольник АВ₁С₁, у которого

|AB₁| = |A^’B^’|, Ð A 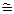ÐA^’, ÐВ₁ = Ð В, ÐС₁ = Ð С.

Треугольники АВ₁С₁ и А^¢B^¢C^¢ равны. Это значит, что треугольник А^¢B^¢C^¢ есть образ треугольника АВ₁С₁ при некотором движении .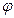

Следовательно, он является образом треугольника АВС при композиции гомотетии 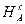и движения 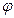, т.е. при преобразовании подобия.

▄