Применение подобий к решению задач

Задача 1. В данный прямоугольный треугольник вписать квадрат так, чтобы три его вершины лежали на катетах, а четвёртая на гипотенузе.

Решение. Пусть С – вершина прямого угла треугольника АВС. Построим произвольный квадрат CKLM так, чтобы точки К и М лежали соответственно на сторонах СА и СВ (или их продолжениях). Проведём луч CL и обозначим через О точку его пересечения с гипотенузой АВ. Из точки О опустим перпендикуляры ОР и ОQ на катеты СА и СВ. Четырёхугольник СРOQ – искомый.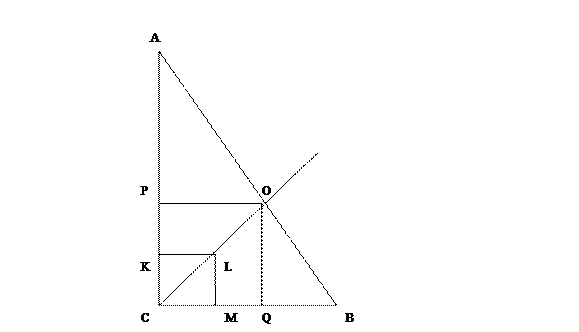

Доказательство. Легко видеть, что четырёхугольник СРOQ гомотетичен прямоугольнику CKLM. Коэффициент гомотетии равен отношению 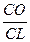, центр гомотетии- точка С.

Используя подобие, докажем ещё теорему о точке пересечения медиан треугольника.

Задача 2. Медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении 2:1, считая от вершины.

Доказательство. Пусть медианы АМ и BN треугольника АВС пересекаются в точке О. Тогда проведём среднюю линию MN. Поскольку MN || АВ и MN = 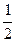АВ, то треугольник ОАВ подобен треугольнику OMN с коэффициентом подобия 2. Следовательно, АО: ОМ = ВО: ОN = 2.

Медиана СР также проходит через точку О. Действительно, если повторить проведённые рассуждения для АМ и СР, то снова получим, что они пересекаются в точке, которая делит АМ в отношении 2:1. Этой точкой является точка О. Поэтому СР проходит через О.

▄