Аффинные преобразования плоскости

Определение 1. Пусть R = (О 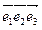) и R¢ = (О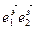^’ ) два аффинных репера заданного аффинного пространства. Рассмотрим соответствие, при котором каждой точке М пространства, имеющей в R координаты (х, у) соответствует точка М¢, имеющая в R¢ те жекоординаты (х, у).

Очевидно, что рассматриваемое соответствие есть преобразование плоскости, которое мы в дальнейшем будем называть аффинным преобразованием.

Так как аффинное преобразование плоскости сохраняет координаты точек в новом репере, то оно сохраняет простое отношение трех точек (М₁ М₂, М₃) = (М₁¢М₂¢, М₃¢), а, следовательно, отображает прямую в прямую. Нетрудно видеть, что аффинное преобразование плоскости сохраняет параллельность прямых на плоскости.

Очевидно, что любое преобразование подобия, в частности любое движение, является аффинным преобразованием.

Покажем, что существуют аффинные преобразования, отличные от подобий. Рассмотрим следующий пример.

Зададим в плоскости s прямую l и выберем положительное число k. Определим преобразование плоскости f следующим образом: каждой точке М плоскости s поставим в соответствие точку М¢ так, чтобы

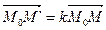, (1)

где М₀ – ортогональная проекция точки М на прямую l.

Из равенства (1) следует, что

,

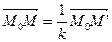поэтому каждая точка М¢ плоскости имеет один и только один прообраз. Следовательно, мы имеем преобразование плоскости.

Рассмотрим точку N и ее образ N¢. Тогда

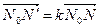. (2)

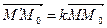Из (1) . (3)

Тогда 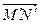= 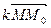+ + 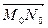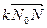. Очевидно, 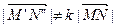. Следовательно, данное преобразование не является подобием плоскости. С другой стороны, это преобразование можно задать двумя реперами R = O 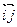и R' = O 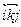, если за ось абсцисс выбрать данную прямую l.

.