Даны параллельные прямые а и b, пересекающая их прямая с и отрезок длины m, так, чтобы его вершины лежали соответственно на данных прямых.
Решение:
Анализ. Пусть искомый треугольник АВС построен: А 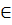 а, В
а, В 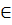 b, C
b, C 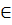 c, и
c, и 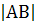 =
= 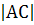 =
= 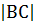 = m (рис.1),
= m (рис.1),
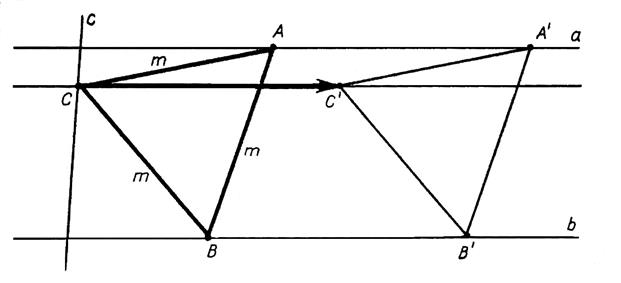
рис. 1
выполним перенос 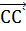 треугольника АВС, причём
треугольника АВС, причём 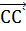 = а. Получим треугольник
= а. Получим треугольник 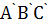 со сторонами данной длины m, причём
со сторонами данной длины m, причём 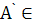 а,
а, 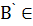 b.
b.
Так как треугольник 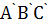 , две вершины которого лежат на прямых а и b, построить нетрудно, то на этом анализ можно закончить. Таким образом, задачу можно свести к построению равностороннего треугольника
, две вершины которого лежат на прямых а и b, построить нетрудно, то на этом анализ можно закончить. Таким образом, задачу можно свести к построению равностороннего треугольника 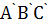 со стороной длины m, причём
со стороной длины m, причём 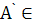 а,
а, 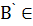 b, а затем к последующему параллельному переносу
b, а затем к последующему параллельному переносу 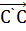 треугольника
треугольника 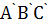 , причём конец С вектора
, причём конец С вектора 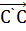 определяется как точка пересечения прямой
определяется как точка пересечения прямой 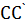 = а с данной прямой с.
= а с данной прямой с.
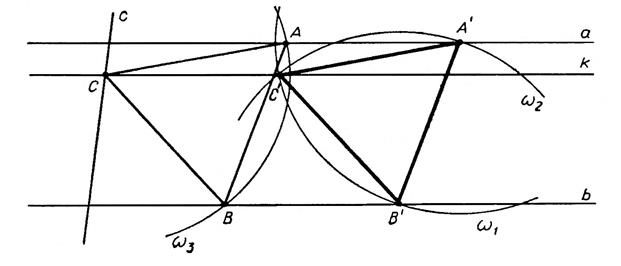
рис. 2
Построение (рис.2) Выбираем произвольную точку 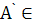 а. Описываем окружность
а. Описываем окружность 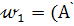 , m). Находим точку
, m). Находим точку 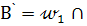 b. Описываем окружность
b. Описываем окружность 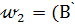 , m). Находим точку
, m). Находим точку 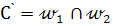 . Через точку
. Через точку 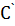 проводим прямую k
проводим прямую k 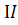 а и находим точку С= k
а и находим точку С= k 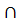 с. Откладываем
с. Откладываем 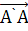 =
= 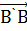 =
= 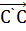 и получаем треугольник АВС.
и получаем треугольник АВС.
Доказательство. По построению треугольник 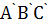 удовлетворяет всем поставленным условиям, кроме условия
удовлетворяет всем поставленным условиям, кроме условия 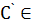 с. После параллельного переноса
с. После параллельного переноса 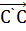 удовлетворяет и это условие. Таким образом,
удовлетворяет и это условие. Таким образом, 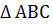 - искомый.
- искомый.
Исследование. При выбранном способе построения число решений задачи зависит прежде всего от числа точек 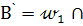 b. Если радиус m окружности
b. Если радиус m окружности 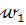 больше расстояния h между прямыми а и b, то таких точек две.
больше расстояния h между прямыми а и b, то таких точек две.
Если m = h, то окружность 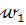 касается прямой b и тогда точка пересечения одна.
касается прямой b и тогда точка пересечения одна.
Если же m 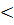 h, то окружность
h, то окружность 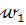 и прямая b не пересекаются. Окружности
и прямая b не пересекаются. Окружности 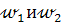 всегда имеют общие точки, так как по построению
всегда имеют общие точки, так как по построению 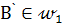 ,
, 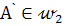 . Значит, при любом выборе точки
. Значит, при любом выборе точки 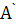 образуются две точки пересечения окружностей
образуются две точки пересечения окружностей 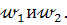
Итак, возможны три следующих случая:
1) Если m 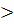 h, то задача имеет четыре решения (рис. 3а),
h, то задача имеет четыре решения (рис. 3а),
2) Если m 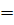 h, то задача имеет два решения (рис. 3б)
h, то задача имеет два решения (рис. 3б)
3) Если m 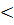 h, то задача не имеет решений.
h, то задача не имеет решений.
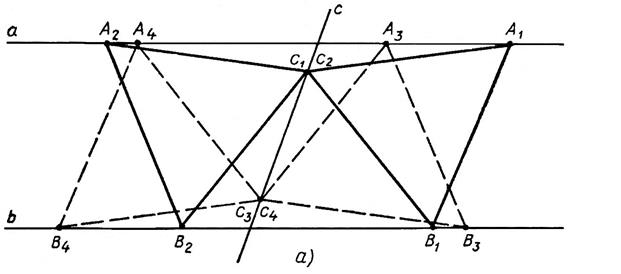
рис. 3а
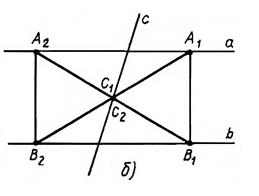
рис. 3б
 2015-07-04
2015-07-04 425
425








