2015-07-04
1141
1. Обозначим через А множество всех аффинных преобразований плоскости. Если f1 Î А и f2 Î A, то очевидно f2 f1 Î A. Докажем, что если f Î A, то f -1 Î A. Действительно, пусть А, В и С – три точки, лежащие на одной прямой, и (АВ, С) =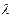 
. Рассмотрим образы точек А и В: А¢ = f -1(A), B¢ = f -1(B). На прямой A¢B¢ возьмём точку С¢ так, чтобы (A¢B¢, С¢) = 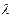, и докажем, что С¢ = f -1 (С). Так как f – аффинное преобразование, то (f (A¢) f (B¢), f (С¢)) = 
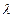или (АВ, f (С’)) = 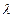. Таким образом, (АВ, С) = (АВ, f (С’)), т.е. С = f (C’) или С¢= f -1 (С).
Итак, множество А всех аффинных преобразований плоскости образует группу. Она называется группой аффинных преобразований.
Рассмотрим важнейшие подгруппы этой группы.
а) Пусть Р – множество всех подобий плоскости. Если g Î Р и f Î Р, то, очевидно, f ◦g Î Р. Далее, если g Î Р, то и g –1 Î Р. Таким образом, множество Р является группой преобразований. Она называется группой преобразований подобия плоскости (или, короче, группой подобий). Ясно, что группа подобий является подгруппой группы аффинных преобразований.
б) Пусть D – множество всех движений плоскости. Если g Î D и f Î D, то, очевидно, f Î D. Далее, если g Î D, то g -1 Î D. Таким образом, множество D является группой. Она называется группой движений плоскости. Эта группа является подгруппой группы подобий, а также подгруппой группы аффинных преобразований.
Другими примерами подгрупп аффинных преобразований являются:
в) множество всех аффинных преобразований первого рода;
г) множество всех аффинных преобразований плоскости, каждое из которых оставляет фиксированную точку О неподвижной (группа центро – аффинных преобразований);
е) множество всех параллельных переносов (группа переносов плоскости).
2. Теория геометрических преобразований сыграла важную роль в формировании взглядов на геометрию. Если проанализировать основные определения, теоремы и другие утверждения, известные нам из курса геометрии, то можно прийти к выводу, что по существу в геометрии изучаются те свойства геометрических фигур, которые остаются неизменными при определённой группе геометрических преобразований. В большинстве случаев такой группой является группа подобий или группа движений.
Эти наблюдения не случайны. Теория геометрических преобразований лежит в основе общего определения геометрии, позволяющего разобраться в сходствах и различиях между разными ветвями этой математической дисциплины.
Так чем же занимается геометрия? Рассмотрим общую схему, лежащую в основе определения геометрии.
Пусть дана группа преобразований G некоторого непустого множества Е. Любое подмножество множества Е мы называем фигурой. Напомним, что две фигуры F и F¢ называются G – эквивалентными, если в группе G существует такое преобразование f, что F¢ = f(F). Понятие G – эквивалентности является отношением эквивалентности на множестве всех подмножеств множества Е. Для конкретных групп преобразований термин «G – эквивалентность» заменяется другим термином. Например, если Е – точечное пространство, а G – группа движений, то «G – эквивалентность» заменяется термином «равенство» или «конгруэнтность». Если G – подобие, то «G – эквивалентность» заменяется термином «подобие», а если G – группа аффинных преобразований, то термином «аффинная эквивалентность».
Пусть F – данная фигура. Те свойства этой фигуры, которые сохраняются при любых преобразованиях из группы G, т.е. свойства, общие для F и любой другой фигуры F¢, которая G – эквивалентна F, называются инвариантными свойствами фигуры F относительно группы G. Так, свойство фигуры в пространстве быть плоскостью является ее инвариантным свойством относительно группы А. Свойство фигуры лежать в плоскости также является инвариантным свойством. Простое отношение трех точек прямой является основным инвариантным свойством группы А. Мера угла – основной инвариант группы подобий, а длина отрезка – основной инвариант группы движений.
Теперь мы можем дать общее определение геометрии.
Геометрия – это наука, изучающая такие свойства фигур, которые остаются инвариантными при всех преобразованиях некоторой группы G.
Из этого определения следует, что если две фигуры G – эквивалентны, то они обладают одними и теми же свойствами, которые называются геометрическими. Отсюда вытекает также, что в принципе можно построить много различных геометрий, так как много различных групп преобразований.
Такой взгляд на геометрию был впервые сформулирован известным немецким математиком Феликсом Клейном в его работе «Эрлангенская программа», изданной в 1872 г..
Среди различных геометрий наиболее распространенными являются аффинная геометрия и евклидова геометрия. Их группами преобразований являются группа аффинных преобразований и группа движений. Каждая из этих геометрий является вполне содержательной и самостоятельной наукой. В аффинной геометрии можно говорить о точках, прямых и плоскостях и их взаимном расположении. Однако, такие понятия как равнобедренный треугольник, прямоугольник, прямоугольный параллелепипед, сфера отсутствуют в этой геометрии. Эти понятия относятся к евклидовой геометрии, в которой основной группой считается группа подобий или можно говорить о группе движений. Так теорема Пифагора относится к евклидовой геометрии, но не является объектом изучения в аффинной геометрии.
