Задание №4

Дана прямая l и две точки Р и Q по одну сторону от l. Найдём на прямой l такую точку Х, чтобы периметр треугольника РQХ был наименьшим.

Решение:

Анализ. Пусть точка М – некоторая точка данной прямой l. Построим точку 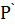, симметричную точке Р относительно прямой l (рис. 1)

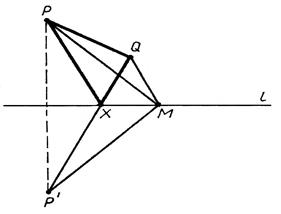
рис. 1

Тогда так как 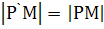, то периметр треугольника РQМ равен: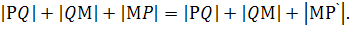

Отрезок РQ фиксированный, поэтому минимум периметра треугольника РQМ достигается при минимуме суммы 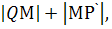т.е. тогда, когда точки Q, М и 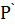лежат на одной прямой. Итак, задачу можно свести к нахождению точки пересечения прямых l и Q 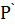, где =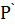

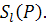
Построение. Строим точку 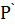= 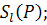проводим прямую 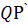и находим точку Х= l 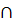Q .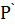

Доказательство. Пусть М – некоторая точка прямой l, отличная от Х. Так как 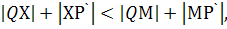то 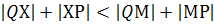, а значит, и 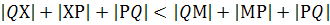. Таким образом, точка Х искомая.

Исследование. Если прямая РQ не перпендикулярна прямой l, то задача имеет единственное решение.

Если (РQ) 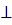l, то решений нет.