Выполним параллельный перенос 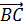 диагонали ВD (рис. 1).
диагонали ВD (рис. 1).

Рис 1
При этом точка D отобразиться в точку Е, такую, что 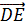 =
= 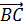 . Площади треугольников АВС и DCE равны, так как у этих треугольников стороны ВС и DЕ, а также высоты, опущенные на эти стороны, конгруэнтны, поэтому
. Площади треугольников АВС и DCE равны, так как у этих треугольников стороны ВС и DЕ, а также высоты, опущенные на эти стороны, конгруэнтны, поэтому
SABCD = S∆ACD + S∆ABC = S∆ACD + S∆DCE = S∆ACE
и, следовательно,
S∆AOD: SABCD = S∆AOD: S∆ACE.
Последнее отношение легко найти, так как ∆AOD ∆ACE, а площади подобных треугольников относятся как квадраты сходственных сторон:
S∆AOD: S∆ACE = 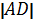 2 :
2 : 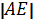 2 = a2: (a + b)2.
2 = a2: (a + b)2.
 2015-07-04
2015-07-04 432
432








