2015-01-21
914
Логарифмы. Пусть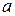 
(основание логарифма) и 
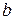положительные числа, причем 
отлично от 1. Запись 
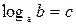равнозначна записи 
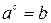, так что имеем тождество: 
.
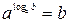Основные свойства логарифмов.
| 1. | 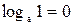 | 2. |  |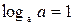
| 3. |  | 4. |  |
| 5. |  | 6. |  |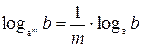
| 7. | 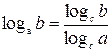 | 8. |  |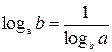
Функция 
, 
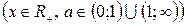называется логарифмической функцией.
Логарифмическая функция является обратной по отношению к показательной функции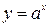 
. Поэтому их графики симметричны относительно биссектрисы I и III координатных углов (рис. 8).
 |  |
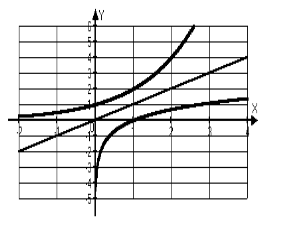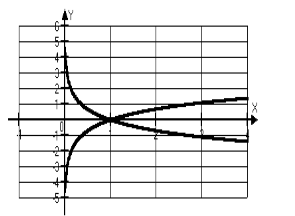| Рис. 8. |
Приведем основные свойства логарифмической функции:
1) Область определения: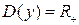 
.
2) Область значений функции: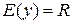 
.
3) Логарифм единицы равен нулю, логарифм основания равен единице: , .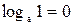
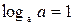4) Функция , 
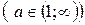возрастает в промежутке 
(рис. 8 а). При этом, логарифмы чисел, больших единицы, положительны, а - меньших единицы, отрицательны.
5) Функция , 
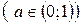убывают в промежутке (рис. 8 б). При этом, логарифмы чисел, меньших единицы, положительны, а - больших единицы, отрицательны.
Уравнение или неравенство, содержащее переменную в показателе степени, называется показательным.
Если число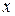 
представлено алгебраическим выражением, содержащим некоторые числа, то найти логарифм этого выражения – значит выразить логарифм числа 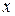через логарифмы этих числа. Нахождение положительного числа по его логарифму называют потенцированием.
Простейшее показательное уравнение имеет вид: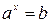 
, где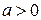 
, 
, 
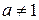. Уравнение имеет единственное решение. При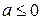 
уравнение не имеет решений.
Если показательное уравнение можно привести к виду 
, то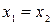 
.
Простейшее логарифмическое уравнение имеет вид: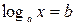 
, где 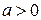, , 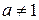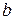- любое действительное число. Тогда уравнение имеет единственное решение 
.
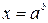Уравнение вида 
, 
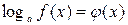, где 
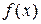и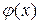 
- алгебраические или трансцендентные функции, решаются, как правило, графически.
Пояснения к разделу:
