Здесь носителем информации является гармоническое колебание высокой частоты 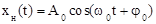 , где
, где 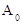 – амплитуда,
– амплитуда, 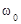 – несущая частота,
– несущая частота, 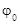 – начальная фаза. Информационным сигналом
– начальная фаза. Информационным сигналом 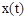 можно воздействовать на любой из параметров: или
можно воздействовать на любой из параметров: или 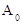 , или
, или 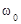 , или
, или 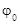 . В результате получают три вида модуляции.
. В результате получают три вида модуляции.
1. Aмплитудная модуляция (АМ). Амплитуда меняется так:
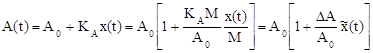 ,
,
где 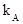 – коэффициент, характеризующий влияние
– коэффициент, характеризующий влияние 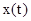 на амплитуду;
на амплитуду;
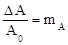 – коэффициент модуляции, характеризует ее глубину;
– коэффициент модуляции, характеризует ее глубину;
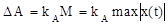 – девиация амплитуды;
– девиация амплитуды;
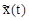 – нормированный сигнал (
– нормированный сигнал (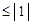 ).
).
Тогда в аналитической форме АМ-сигнал можно записать так:
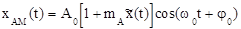 .
.
2. Частотная модуляция (ЧМ). Частота меняется так:
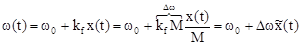 ,
,
где 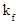 – коэффициент, характеризующий влияние
– коэффициент, характеризующий влияние 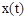 на частоту;
на частоту; 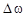 – девиация частоты.
– девиация частоты.
Обозначим: 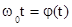 . Представим носитель в другой форме:
. Представим носитель в другой форме: 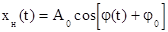 , где
, где 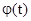 – мгновенная фаза. Связь между мгновенной фазой и частотой имеет вид
– мгновенная фаза. Связь между мгновенной фазой и частотой имеет вид
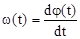 ;
; 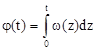 .
.
При ЧМ мгновенная фаза меняется по закону
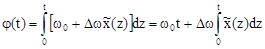 .
.
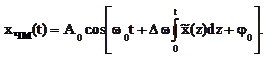 Тогда ЧМ-сигнал можно записать в виде
Тогда ЧМ-сигнал можно записать в виде
3. Фазовая модуляция (ФМ). Фаза изменяется так:
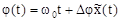 , где
, где 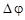 – девиация фазы, причем
– девиация фазы, причем 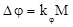 .
.
Тогда ФМ-сигнал имеет вид 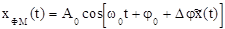 .
.
Рассмотрим пример, когда 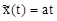 ;
; 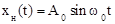 ,
, 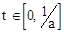 (рис2.102).
(рис2.102).
 |
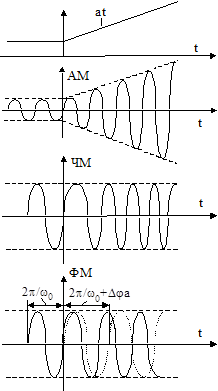
Для данного примера при ФМ частота изменилась с 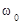 до
до 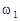 и осталась постоянной.
и осталась постоянной.
ЧМ и ФМ – это частные случаи более общей угловой модуляции (УМ).
УМ – это изменение мгновенной фазы 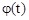 носителя информационным сигналом
носителя информационным сигналом 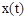 .
.
При ЧМ фаза 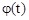 меняется за счет изменения частоты
меняется за счет изменения частоты 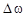 . При ФМ она меняется за счет изменения непосредственно фазы
. При ФМ она меняется за счет изменения непосредственно фазы 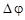 .
.
Рассмотрим спектры сигналов при непрерывной модуляции.
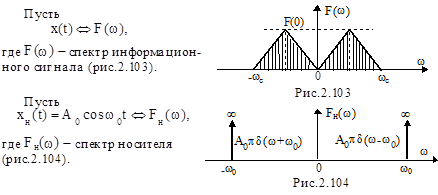
1. Спектр АМ-сигнала. В этом случае АМ-сигнал представляется так:
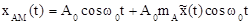 .
.
Отсюда следует, что его спектр (рис.2.105) есть сумма двух спектров (принцип суперпозиции): спектра носителя (первое слагаемое) и с учетом множителя 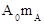 спектра информационного сигнала
спектра информационного сигнала 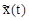 , перенесенного на частоты
, перенесенного на частоты 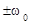 c уменьшенной в 2 раза амплитудой спектра согласно теореме о переносе спектра (второе слагаемое).
c уменьшенной в 2 раза амплитудой спектра согласно теореме о переносе спектра (второе слагаемое).
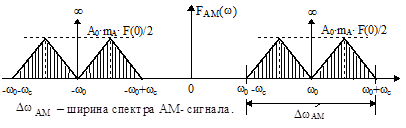
Рис.2.105
2. Спектр ЧМ-сигнала. В общем виде найти этот спектр трудно. Однако для практики это и не нужно. Достаточно знать:
а) что при частотной модуляции спектр информационного сигнала 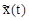 переносится на несущую частоту
переносится на несущую частоту 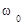 ;
;
|
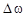 .
. Установлено, что практическая ширина спектра ЧМ-сигнала определяется выражением
|
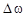 =
= 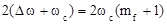 ,
, где 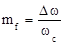 – коэффициент, или индекс частотной модуляции;
– коэффициент, или индекс частотной модуляции; 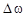 – девиация частоты.
– девиация частоты.
При 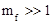 имеем широкополосную ЧМ. Тогда
имеем широкополосную ЧМ. Тогда
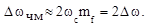
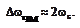 При
При 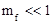 имеем узкополосную ЧМ. Тогда.
имеем узкополосную ЧМ. Тогда.
3. Спектр ФМ-сигнала. При ФМ спектр информационного сигнала 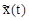 также переносится на несущую частоту
также переносится на несущую частоту 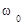 . Практическая ширина спектра ФМ-сигнала также определяется выражением
. Практическая ширина спектра ФМ-сигнала также определяется выражением
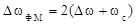 .
.
 2015-07-04
2015-07-04 2794
2794
