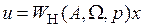 ,
,
где “передаточная функция” нелинейного элемента
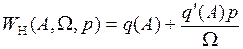 . (1.17)
. (1.17)
В качестве примера рассмотрим нелинейность типа “идеальное реле”, на выходе которого формируется прямоугольный сигнал (рис. 1.17). При этом для
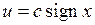
найдем выражения коэффициентов
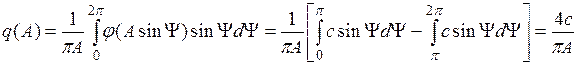 ,
,
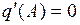 .
.
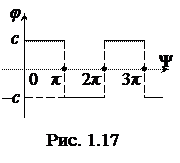
Для других нелинейностей коэффициенты гармонической линеаризации приведены в соответствующих таблицах, входящих в приложения работ [1-5,7].
Введение передаточной функции нелинейного элемента 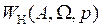 для автоколебательного режима позволяет проводить динамическое исследование НСАУ в автоколебательном режиме на основе известных методов, разработанных для линейных САУ. Поскольку частному решению линейных систем
для автоколебательного режима позволяет проводить динамическое исследование НСАУ в автоколебательном режиме на основе известных методов, разработанных для линейных САУ. Поскольку частному решению линейных систем 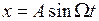 соответствует наличие пары чисто мнимых сопряженных корней
соответствует наличие пары чисто мнимых сопряженных корней 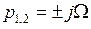 , то необходимое условие существования автоколебаний в НСАУ есть требование существования пары чисто мнимых корней для характеристического уравнения гармонически линеаризованной замкнутой системы
, то необходимое условие существования автоколебаний в НСАУ есть требование существования пары чисто мнимых корней для характеристического уравнения гармонически линеаризованной замкнутой системы
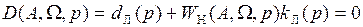 . (1.18)
. (1.18)
На плоскости 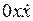 автоколебаниям
автоколебаниям 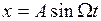 ,
, 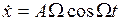 соответствует семейство эллипсов
соответствует семейство эллипсов
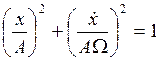
(особая точка типа “центр”).
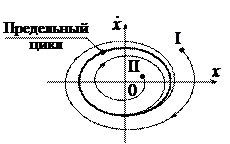
Автоколебания считаются устойчивыми, если любые фазовые траектории, начинающиеся вне предельного цикла (семейство I) и внутри предельного цикла (семейство II), притягиваются к предельному циклу (рис. 1.18).
Рис. 1.18
Рассмотрим далее методы нахождения параметров автоколебаний и исследования их устойчивости.
1.4.1. Метод нахождения параметров автоколебаний и исследование их устойчивости с помощью критерия Михайлова. Для гармонически линеаризованного характеристического уравнения (1.18) делается замена 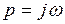 и записывается выражение кривой Михайлова
и записывается выражение кривой Михайлова
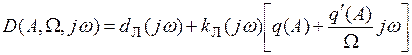 , (1.19)
, (1.19)
где параметр 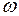 (частота) изменяется в пределах
(частота) изменяется в пределах 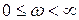 .
.
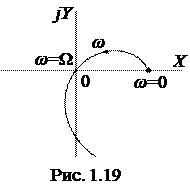 Искомое периодическое решение
Искомое периодическое решение 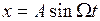 и параметры автоколебаний
и параметры автоколебаний 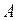 ,
, 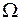 определяются из условия прохождения кривой Михайлова через начало координат
определяются из условия прохождения кривой Михайлова через начало координат
(рис. 1.19), что соответствует уравнению
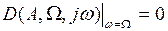 . (1.20)
. (1.20)
Так как в точке прохождения кривой Михайлова через начало координат 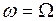 , то для удобства решения можно заранее отождествить в выражении (1.19) значения
, то для удобства решения можно заранее отождествить в выражении (1.19) значения 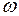 и
и 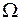 , т.е. применять уравнение:
, т.е. применять уравнение:
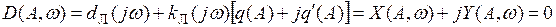 ,
,
эквивалентное системе двух нелинейных алгебраических уравнений
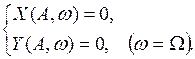 (1.21)
(1.21)
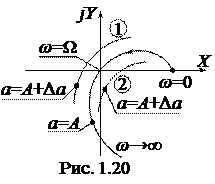 Параметры автоколебаний определяются как вещественные положительные решения
Параметры автоколебаний определяются как вещественные положительные решения 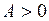 ,
, 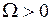 системы (1.21).
системы (1.21).
Для исследования устойчивости периодического решения с амплитудой 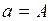 дадим малое приращение
дадим малое приращение 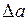 амплитуде. Тогда при
амплитуде. Тогда при 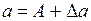 кривая Михайлова займет положение 1, или положение 2 (рис. 1.20).
кривая Михайлова займет положение 1, или положение 2 (рис. 1.20).
При этом, как следует из теории линейных систем [3], кривая 1, охватывающая начало координат, соответствует затухающим колебаниям переходного процесса, а кривая 2 – расходящимся колебаниям.
Поэтому если при 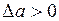 кривая Михайлова займет положение 1, а при
кривая Михайлова займет положение 1, а при 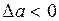 – положение 2, то переходный процесс в системе будет таким, что колебания с амплитудой, больше чем
– положение 2, то переходный процесс в системе будет таким, что колебания с амплитудой, больше чем 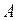 , затухают, а колебания с амплитудой меньше чем
, затухают, а колебания с амплитудой меньше чем 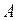 , расходятся. Следовательно, фазовые траектории с обеих сторон сходятся к исследуемому периодическому процессу с амплитудой
, расходятся. Следовательно, фазовые траектории с обеих сторон сходятся к исследуемому периодическому процессу с амплитудой 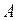 (предельному циклу), что означает устойчивость автоколебаний. Для того чтобы узнать, примет ли кривая Михайлова при
(предельному циклу), что означает устойчивость автоколебаний. Для того чтобы узнать, примет ли кривая Михайлова при 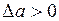 положение 1, достаточно определить, куда будет перемещаться с увеличением амплитуды та точка кривой Михайлова
положение 1, достаточно определить, куда будет перемещаться с увеличением амплитуды та точка кривой Михайлова 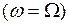 , которая при
, которая при 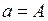 находится в начале координат. Это направление перемещения точки
находится в начале координат. Это направление перемещения точки 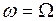 из начала координат с увеличением амплитуды определяется следующими проекциями на координатные оси:
из начала координат с увеличением амплитуды определяется следующими проекциями на координатные оси:
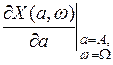 ;
; 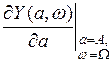 .
.
Касательная к кривой Михайлова имеет направление, которое определяется проекциями
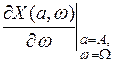 ;
; 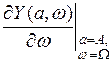 .
.
Перемещение точки 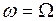 ,
, 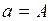 из начала координат за счет изменения амплитуды
из начала координат за счет изменения амплитуды 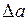 и частоты
и частоты 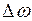 определяется соответственно векторами
определяется соответственно векторами 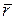 и
и 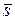 , где
, где
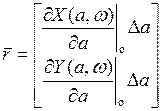 ;
; 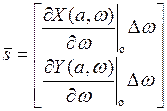 ;
;
символ 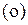 означает вычисление производных на периодическом движении
означает вычисление производных на периодическом движении 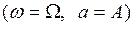 .
.
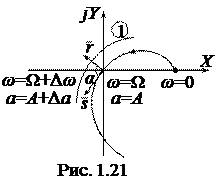 1°. Рассмотрим случай
1°. Рассмотрим случай 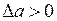 ,
, 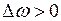
(рис 1.21). Из взаимного расположения векторов 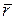 и
и 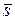 определяется непосредственно устойчивость или неустойчивость исследуемого периодического решения. При этом случай устойчивости автоколебаний соответствует значению угла
определяется непосредственно устойчивость или неустойчивость исследуемого периодического решения. При этом случай устойчивости автоколебаний соответствует значению угла 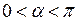 и, следовательно,
и, следовательно, 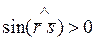 .
.
Оценив знак 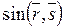 можно с помощью модуля векторного произведения, который в нашем случае можно представить в виде
можно с помощью модуля векторного произведения, который в нашем случае можно представить в виде
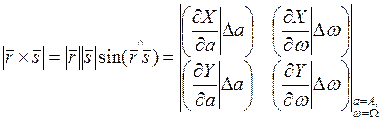 (1.22)
(1.22)
и, учитывая, что 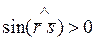 , раскрыв определитель, получим необходимое условие устойчивости автоколебаний:
, раскрыв определитель, получим необходимое условие устойчивости автоколебаний:
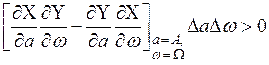 . (1.23)
. (1.23)
Так как 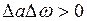 , то из неравенства (1.23) следует неравенство
, то из неравенства (1.23) следует неравенство
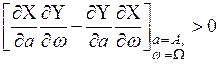 . (1.24)
. (1.24)
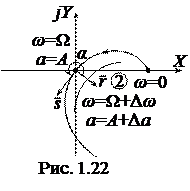 2°. Рассмотрим случай
2°. Рассмотрим случай 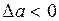 ,
, 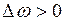
(рис. 1.22). Случай устойчивости автоколебаний соответствует взаимному расположению векторов 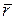 и
и 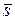 , при котором
, при котором 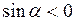 .
.
При учете, что 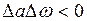 , получаем необходимое условие устойчивости автоколебаний (1.24).
, получаем необходимое условие устойчивости автоколебаний (1.24).
Анализ устойчивости автоколебаний для случаев 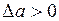 ,
, 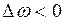 и
и 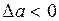 ,
, 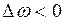 также приводит к условию (1.24).
также приводит к условию (1.24).
Аналитический способ определения параметров автоколебаний и исследования их устойчивости на основе выражений (1.21), (1.24) обычно реализуется на практике, для невысокого порядка характеристического уравнения (1.18).
1.4.2. Метод нахождения параметров автоколебаний и исследование их устойчивости с помощью критерия Найквиста. Рассматривается замкнутая гармонически линеаризованная НСАУ (рис.1.23).
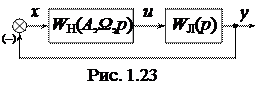 Передаточная функция разомкнутой системы с единичной отрицательной обратной связью
Передаточная функция разомкнутой системы с единичной отрицательной обратной связью
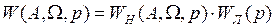 .
.
Незатухающие синусоидальные колебания 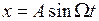 взамкнутой системе согласно частотному критерию устойчивости Найквиста определяются прохождением АФЧХ разомкнутой системы через точку
взамкнутой системе согласно частотному критерию устойчивости Найквиста определяются прохождением АФЧХ разомкнутой системы через точку 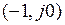 , т.е. равенством
, т.е. равенством
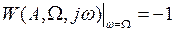 . (1.25)
. (1.25)
Для приближенной передаточной функции нелинейного элемента при подстановке 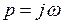 , получим эквивалентную частотную характеристику нелинейного элемента
, получим эквивалентную частотную характеристику нелинейного элемента
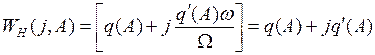 при
при 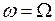 . (1.26)
. (1.26)
Решая уравнение (1.25), получим 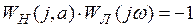 при
при 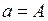 ,
, 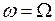 и соответственно
и соответственно
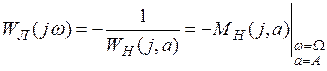 , (1.27)
, (1.27)
где 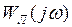 – АФЧХ линейной части.
– АФЧХ линейной части.
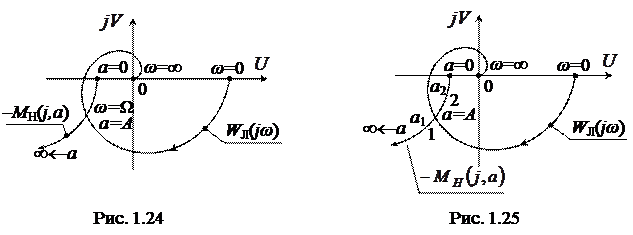
Решения уравнения (1.27) можно находить графически, как точки пересечения кривой 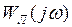 , построенной при изменении частоты
, построенной при изменении частоты 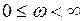 и характеристики
и характеристики 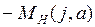 , построенной при изменении
, построенной при изменении 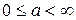 (метод Л.С.Гольдфарба). Построение ведется на комплексной плоскости (рис. 1.24).
(метод Л.С.Гольдфарба). Построение ведется на комплексной плоскости (рис. 1.24).
Точки пересечения двух кривых определяют амплитуду и частоту возможных автоколебаний.
Устойчивость найденного периодического решения оценивается следующим образом. Дается малое приращение амплитуде: 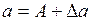 . Тогда при положительном
. Тогда при положительном 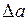 получим на кривой
получим на кривой 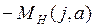 точку 1 (рис.1.25), а при отрицательном
точку 1 (рис.1.25), а при отрицательном 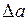 – точку 2. Для устойчивости автоколебаний требуется, чтобы при положительном
– точку 2. Для устойчивости автоколебаний требуется, чтобы при положительном 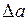 колебания затухали, а при отрицательном
колебания затухали, а при отрицательном 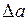 – расходились.
– расходились.
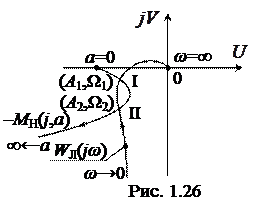 Для этого, согласно критерию Найквиста (в случае устойчивой или нейтральной разомкнутой системы), требуется, чтобы АФЧХ разомкнутой гармонически линеаризованной системы
Для этого, согласно критерию Найквиста (в случае устойчивой или нейтральной разомкнутой системы), требуется, чтобы АФЧХ разомкнутой гармонически линеаризованной системы 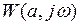 в первом случае не охватывала точку
в первом случае не охватывала точку 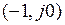 , а во втором– охватывала. Это соответствует тому, чтобы точка с амплитудой
, а во втором– охватывала. Это соответствует тому, чтобы точка с амплитудой 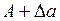 на характеристике
на характеристике 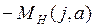 при
при 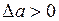 лежала вне, а при
лежала вне, а при 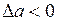 – внутри характеристики
– внутри характеристики 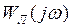 . Автоколебания, соответствующие рис. 1.25 – устойчивы.
. Автоколебания, соответствующие рис. 1.25 – устойчивы.
Автоколебания, соответствующие точке I (рис. 1.26) с параметрами 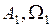 , – неустойчивы, а точке II с параметрами
, – неустойчивы, а точке II с параметрами 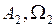 – устойчивы. Отсюда получаем простое правило.
– устойчивы. Отсюда получаем простое правило.
Для того чтобы автоколебания были устойчивы, необходимо чтобы годограф 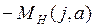 при изменении
при изменении 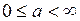 пересекал годограф
пересекал годограф 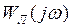 изнутри наружу.
изнутри наружу.
Изложенным графоаналитическим методом удобно пользоваться, привлекая логарифмические частотные характеристики линейной части.
Пусть для однозначной нелинейности 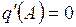 . Тогда уравнение (1.27) примет вид
. Тогда уравнение (1.27) примет вид
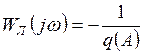 ,
,
откуда следует, что
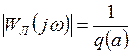 ,
, 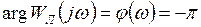 ,
,
и соответственно для ЛАХ и ЛФЧХ линейной части
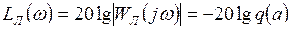 ,
, 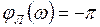 .
.
Решение этих уравнений представлено на рис. 1.27 (точка I).Автоколебания будут устойчивыми, если точке I при приращении амплитуды 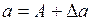 , где
, где 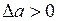 , соответствует значение
, соответствует значение 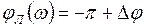 , где
, где 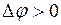 (точка II), а значению
(точка II), а значению 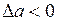 соответствует
соответствует 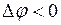 .
.
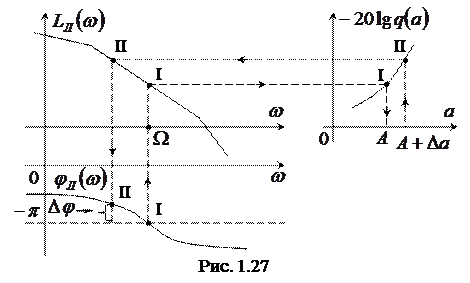 |
Пример 1.2. Рассмотрим нелинейную САУ (рис. 1.28) с нелинейностью типа “ идеальное реле”, где
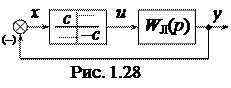
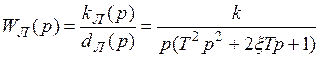 ,
,
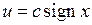 .
.
Коэффициенты гармонической линеаризации 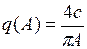 ,
, 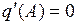 .
.
Характеристический полином замкнутой гармонически линеаризованной системы 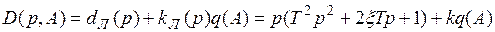 .
.
1° Применение метода, основанного на критерии Михайлова.
Сделаем замену 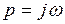 :
:
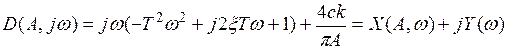 .
.
Получим систему уравнений
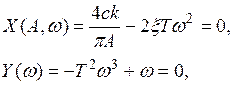
откуда находятся параметры автоколебаний
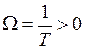 ,
, 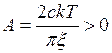 .
.
Проверим условия устойчивости автоколебаний.
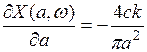 ;
; 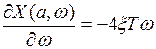 ;
;
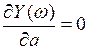 ;
; 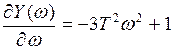 ;
;
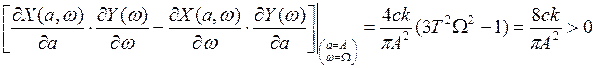 ,
,
таким образом, автоколебания с найденными параметрами устойчивы.
2° Применение графоаналитического метода Гольдфарба.
 2015-07-04
2015-07-04 632
632








