Для исследования устойчивости нелинейных САУ применяется метод функций Ляпунова, который позволяет также строить количественные оценки динамики переходных процессов. Для решения задач абсолютной устойчивости НСАУ широкое применение получил частотный метод В.М. Попова.
1.5.1. Метод функций Ляпунова. Рассматривается математическая модель НСАУ в виде уравнений возмущенного движения, представленная в форме пространства состояний:
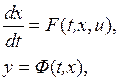 (1.28)
(1.28)
где 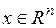 – вектор состояния,
– вектор состояния, 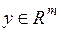 – вектор выхода,
– вектор выхода, 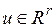 – вектор управления,
– вектор управления, 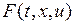 ,
, 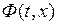 – непрерывные функции в области
– непрерывные функции в области 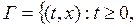
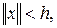
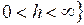 .
.
При предположении, что известно управление 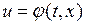 , получаем уравнение возмущенного движения нелинейной замкнутой САУ
, получаем уравнение возмущенного движения нелинейной замкнутой САУ
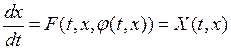
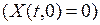 . (1.29)
. (1.29)
Невозмущенному движению системы соответствует нулевое решение 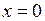 .
.
Если невозмущенное движение 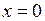 асимптотически устойчиво, то вокруг начала координат
асимптотически устойчиво, то вокруг начала координат 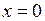 существует область притяжения траектории
существует область притяжения траектории 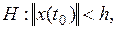 обладающая тем свойством, что все траектории с начальными значениями из области притяжения
обладающая тем свойством, что все траектории с начальными значениями из области притяжения 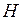 асимптотически притягиваются к невозмущенному движению, т.е.
асимптотически притягиваются к невозмущенному движению, т.е. 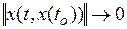 при
при 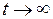 . Если область притяжения достаточно мала, то имеется устойчивость в малом. Если область притяжения
. Если область притяжения достаточно мала, то имеется устойчивость в малом. Если область притяжения 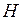 имеет конечные размеры (величина постоянной
имеет конечные размеры (величина постоянной 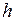 удовлетворяет заданным требованиям), то имеется устойчивость в большом. Если область притяжения совпадает со всем пространством
удовлетворяет заданным требованиям), то имеется устойчивость в большом. Если область притяжения совпадает со всем пространством 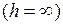 , то имеется устойчивость в целом. Метод функций Ляпунова позволяет не только устанавливать наличие какого-либо типа устойчивости невозмущенного движения, но и строить оценки области притяжения.
, то имеется устойчивость в целом. Метод функций Ляпунова позволяет не только устанавливать наличие какого-либо типа устойчивости невозмущенного движения, но и строить оценки области притяжения.
Для исследования устойчивости нелинейных систем наибольшее распространение получила следующая модификация теоремы Ляпунова об асимптотической устойчивости.
Теорема об асимптотической устойчивости. Невозмущенное движение 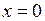 системы (1.29) асимптотически устойчиво, если существует функция Ляпунова
системы (1.29) асимптотически устойчиво, если существует функция Ляпунова 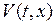 , удовлетворяющая неравенствам
, удовлетворяющая неравенствам
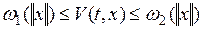 , (1.30)
, (1.30)
производная от которой в силу уравнений возмущенного движения
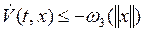 ,
,
где 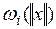
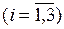 – непрерывные неубывающие функции, такие, что
– непрерывные неубывающие функции, такие, что 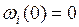 и
и 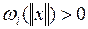 при
при 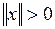 ,
, 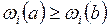 , если
, если 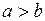 .
.
Здесь 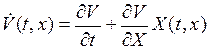 – производная от функции Ляпунова в силу уравнений возмущенного движения (1.29).
– производная от функции Ляпунова в силу уравнений возмущенного движения (1.29).
При указанных в теореме требованиях функция Ляпунова определенно положительна и допускает бесконечно малый высший предел, а ее производная определенно отрицательна.
Наибольший интерес при исследовании нелинейных САУ представляет случай экспоненциальной устойчивости, когда решения уравнения (1.29) удовлетворяют в области 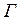 следующей оценке
следующей оценке
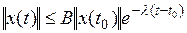 , (1.31)
, (1.31)
где 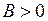 ,
, 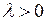 – постоянные.
– постоянные.
Теорема Н.Н.Красовского об экспоненциальной устойчивости. Невозмущенное движение 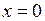 системы (1.29) экспоненциально устойчиво в области
системы (1.29) экспоненциально устойчиво в области 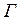 , если существует функция Ляпунова, удовлетворяющая следующим оценкам:
, если существует функция Ляпунова, удовлетворяющая следующим оценкам:
1° 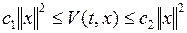 ,
,
2° 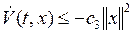 , (1.32)
, (1.32)
3° 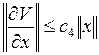 ,
,
где 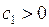 ,
, 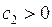 ,
, 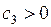 ,
, 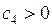 – постоянные.
– постоянные.
Наличие у нелинейной системы свойства экспоненциальной устойчивости гарантирует экспоненциальный характер переходных процессов, что чрезвычайно важно для САУ.
Особое место в различных типах устойчивости САУ занимает абсолютная устойчивость.
Рассмотрим уравнения возмущенного движения САУ, которые приведены к следующему виду
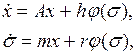 (1.33)
(1.33)
где 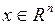 ,
, 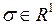 ,
, 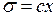 ,
, 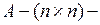 постоянная матрица,
постоянная матрица, 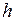 – постоянный столбец,
– постоянный столбец, 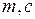 – постоянные строки,
– постоянные строки, 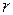 – постоянная. Однозначная непрерывная функция
– постоянная. Однозначная непрерывная функция 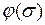 удовлетворяет условиям
удовлетворяет условиям
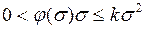
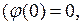
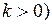 , (1.34)
, (1.34)
то есть принадлежит сектору 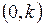 (рис. 1.30).
(рис. 1.30).
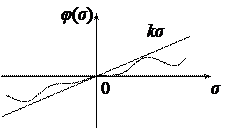
Абсолютная устойчивость – асимптотическая устойчивость в целом нулевого решения системы (1.33), 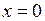 ,
, 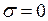 , содержащей нелинейности типа (1.34) (принадлежащие сектору).
, содержащей нелинейности типа (1.34) (принадлежащие сектору).
Рис. 1.30
Решение задачи абсолютной устойчивости может быть произведено с помощью функции Ляпунова специального вида “квадратичная форма плюс интеграл”, предложенной А.И. Лурье и В.К. Постниковым
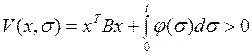 , (1.35)
, (1.35)
где 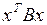 – положительно определенная квадратичная форма.
– положительно определенная квадратичная форма.
Вычисляется производная от функции Ляпунова
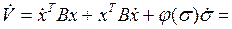
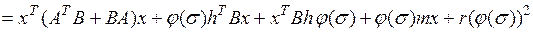 ,
,
которую можно представить в виде
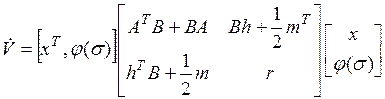 . (1.36)
. (1.36)
Если квадратичная форма (1.36) определенно отрицательна, то невозмущенное движение 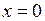 ,
, 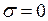 асимптотически устойчиво.
асимптотически устойчиво.
Пример 1.3. Рассмотрим систему
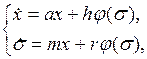
где 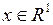 ,
, 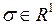 ,
, 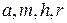 – постоянные.
– постоянные.
Полагая
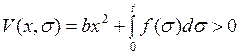
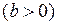 ,
,
найдем
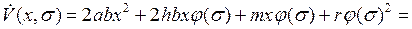
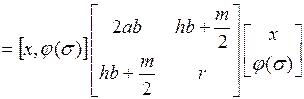 .
.
Достаточные условия абсолютной устойчивости имеют вид
1) 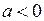 ,
, 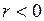
2) 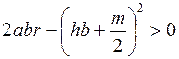 .
.
1.5.2. Абсолютная устойчивость. Частотный критерий В.М.Попова.
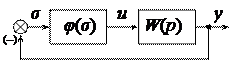 Рассматривается нелинейная САУ, структурная
Рассматривается нелинейная САУ, структурная
схема которой представлена на рис.1.31, где передаточная функция линейной части
Рис. 1.31
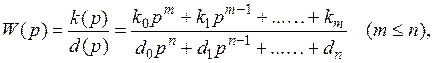
стационарная нелинейность удовлетворяет условиям
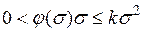
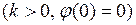
или 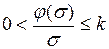 . (1.37)
. (1.37)
Случай 1. Линейная часть САУ устойчива, т.е. характеристическое уравнение
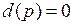 (1.38)
(1.38)
имеет только корни с отрицательными вещественными частями:
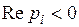 ,
, 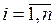 .
.
Критерий Попова. Замкнутая система абсолютно устойчива в классе стационарных непрерывных нелинейностей, удовлетворяющих условиям (1.37), если для некоторого вещественного 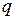 и для всех
и для всех 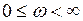 , выполнено неравенство
, выполнено неравенство
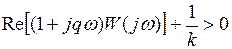 .(1.39)
.(1.39)
Представим комплексный вектор 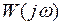 в виде
в виде
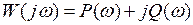 ,
,
где 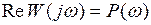 ,
, 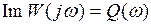 . Тогда неравенство (1.39) примет вид
. Тогда неравенство (1.39) примет вид
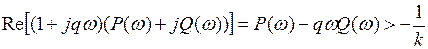 . (1.40)
. (1.40)
Практическая ценность критерия Попова состоит в его простой геометрической интерпретации. Для этого введем преобразованную частотную характеристику 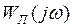 , у которой вещественная часть совпадает с вещественной частью
, у которой вещественная часть совпадает с вещественной частью 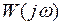 , а мнимая часть отличается на множитель “
, а мнимая часть отличается на множитель “ 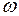 ”:
”:
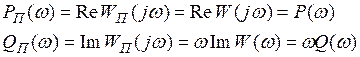 , (1.41)
, (1.41)
Тогда неравенство (1.40) примет вид
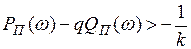 . (1.42)
. (1.42)
Отметим некоторые особенности характеристики 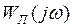 .
.
1º 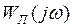 – четная функция “
– четная функция “ 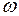 ” и кривая
” и кривая 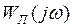 не будет симметричной относительно вещественной оси при изменении
не будет симметричной относительно вещественной оси при изменении 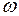 в пределах
в пределах 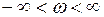 . При
. При 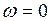 кривые
кривые 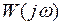 и
и 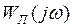 имеют общую точку на положительной вещественной полуоси.
имеют общую точку на положительной вещественной полуоси.
2° Если n–m 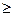 2, то
2, то 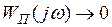 при
при 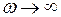 .
.
если n–m= 1, то 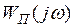
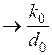 при
при 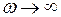 ,
,
где 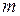 и
и 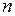 – высшие степени полиномов в передаточной функции
– высшие степени полиномов в передаточной функции 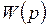 .
.
3° Характеристика 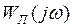 пересекает вещественную ось в тех же точках и при тех же значениях частоты
пересекает вещественную ось в тех же точках и при тех же значениях частоты 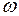 , что и характеристика
, что и характеристика 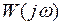 .
.
В результате замены неравенства (1.42) равенством
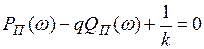 (1.43)
(1.43)
получим в координатах 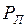 ,
, 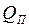 уравнение касательной к характеристике
уравнение касательной к характеристике 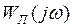 . Прямая проходит через точку
. Прямая проходит через точку 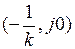 на вещественной оси и имеет угловой коэффициент
на вещественной оси и имеет угловой коэффициент 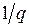 . Кривая
. Кривая 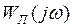 лежит справа от этой прямой.
лежит справа от этой прямой.
Таким образом, геометрическое условие абсолютной устойчивости можно сформулировать следующим образом:
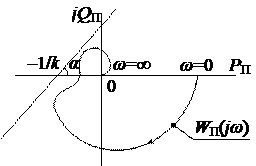 |
Состояние равновесия замкнутой системы с одной стационарной нелинейностью, удовлетворяющей условиям (1.37), абсолютно устойчиво, если на плоскости преобразованной частотной характеристики
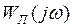 через точку
через точку 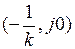 можно провести прямую так, чтобы характеристика
можно провести прямую так, чтобы характеристика 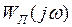 целиком лежала справа от этой прямой (рис.1.32) с углом наклона
целиком лежала справа от этой прямой (рис.1.32) с углом наклона 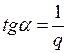 .
. Рис. 1.32
Область, определяющая выбор параметра 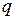 , зависит от свойств нелинейного элемента:
, зависит от свойств нелинейного элемента:
– для непрерывной однозначной стационарной характеристики 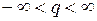 ;
;
– для непрерывной нестационарной и неоднозначной характеристики 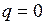 ;
;
– для релейных характеристик типа “идеальное реле” и “реле с зоной нечувствительности” 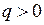 .
.
Замечание. Т ак как преобразованная частотная характеристика 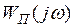 должна пересекать вещественную ось правее точки
должна пересекать вещественную ось правее точки 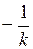 , то и исходная частотная характеристика
, то и исходная частотная характеристика 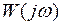 должна также пересекать вещественную ось правее этой точки.
должна также пересекать вещественную ось правее этой точки.
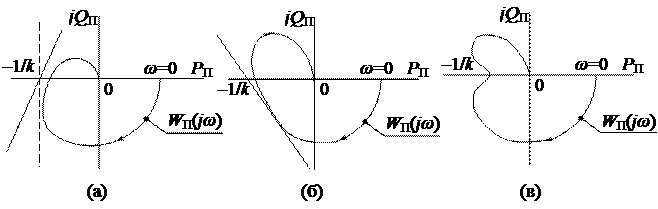
На рис.1.33 показаны случаи, когда условие Попова выполняется при 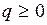 (a),
(a), 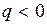 (б), условие не может быть выполнено ни при каких значениях
(б), условие не может быть выполнено ни при каких значениях 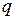 (в).
(в).
Рис.1.33
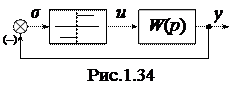 Частный случай. Для нелинейной САУ, содержащей одно идеальное реле (рис.1.34), где
Частный случай. Для нелинейной САУ, содержащей одно идеальное реле (рис.1.34), где 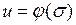 ,
,
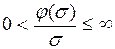 ,
, 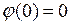 .
.
Условие абсолютной устойчивости при устойчивой линейной части запишется в виде неравенства
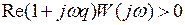 , (1.44)
, (1.44)
при 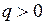 и
и 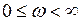 , т.е. характеристика
, т.е. характеристика 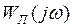 должна лежать правее прямой, проведенной через начало координат с положительным наклоном.
должна лежать правее прямой, проведенной через начало координат с положительным наклоном.
Случай 2. Линейная часть САУ может быть нейтральна или неустойчива, т.е. характеристическое уравнение (1.38) может иметь корни с нулевыми или положительными вещественными частями.
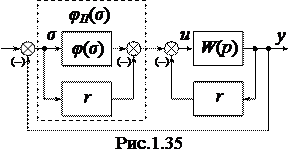 Произведем эквивалентное преобразование исходной нелинейной САУ (рис.1.31), в результате которого получим преобразованную схему (рис.1.35). Схемы рис.1.31, 1.35 эквивалентны по выходу
Произведем эквивалентное преобразование исходной нелинейной САУ (рис.1.31), в результате которого получим преобразованную схему (рис.1.35). Схемы рис.1.31, 1.35 эквивалентны по выходу 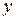 , поскольку на вход
, поскольку на вход 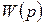 поступает один и тот же сигнал
поступает один и тот же сигнал 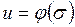
(с учетом 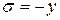 ).
).
Выбирается такое минимальное значение 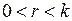 , при котором преобразованная линейная часть устойчива, т.е. для
, при котором преобразованная линейная часть устойчива, т.е. для
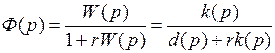 (1.45)
(1.45)
все корни характеристического уравнения
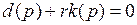 (1.46)
(1.46)
имеют отрицательные вещественные части.
Для преобразованного нелинейного элемента
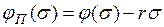 ;
; 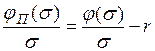 .
.
Потребуем, чтобы в соответствии с критерием Попова нелинейность 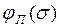 удовлетворяла неравенству
удовлетворяла неравенству
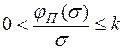 . (1.47)
. (1.47)
Тогда нелинейность 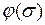 должна относиться к классу нелинейностей, лежащих в секторе
должна относиться к классу нелинейностей, лежащих в секторе 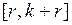 :
:
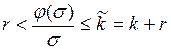 . (1.48)
. (1.48)
Применяя к преобразованной схеме рис.1.35 критерий Попова, получим неравенство
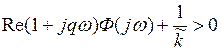 , (1.49)
, (1.49)
в котором по сравнению с (1.39) функция 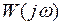 заменена на
заменена на 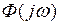 .
.
Частный случай. Рассмотрим случай, когда линейная часть нелинейной САУ является астатической первого порядка, т.е. уравнение (1.38) имеет один вещественный нулевой корень и левые остальные корни. Чтобы все корни характеристического уравнения (1.46) были с отрицательными вещественными частями, достаточно взять значение параметра 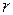 сколь угодно малым. При этом нелинейность
сколь угодно малым. При этом нелинейность 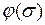 должна удовлетворять условиям
должна удовлетворять условиям
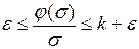 ,
,
где 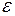 – малая положительная величина.
– малая положительная величина.
Таким образом, практически можно пользоваться условием Попова и в этом случае, только при нелинейностях 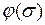 , которые могут не касаться оси абсцисс.
, которые могут не касаться оси абсцисс.
Пример 1.4. Пусть линейная часть САУ имеет передаточную функцию
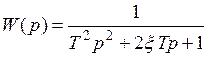 ,
,
где 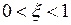 ;
;
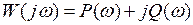 ,
,
где 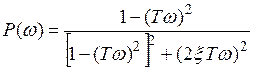 ,
, 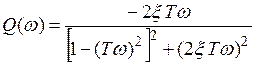 .
.
Амплитудно-фазовая характеристика 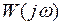 изображена на рис.1.36.
изображена на рис.1.36.
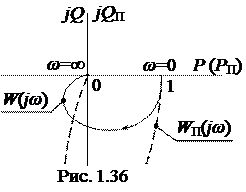 |
Преобразованная частотная характеристика
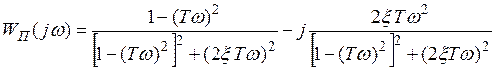 .
.
Характеристика 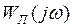 отличается от
отличается от 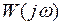 лишь изменением масштаба ординат в
лишь изменением масштаба ординат в 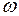 раз. Так как
раз. Так как 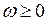 , то при любом таком изменении
, то при любом таком изменении 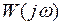 всегда через начало координат можно провести прямую так, чтобы эта характеристика лежала справа от нее. Это означает, что замкнутая нелинейная система будет абсолютно устойчива при любой нелинейности
всегда через начало координат можно провести прямую так, чтобы эта характеристика лежала справа от нее. Это означает, что замкнутая нелинейная система будет абсолютно устойчива при любой нелинейности 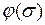 , для которой коэффициент
, для которой коэффициент 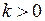 , т.е. расположенной в квадрантах 1 и 3.
, т.е. расположенной в квадрантах 1 и 3.
Пример 1.5. Линейная часть САУ имеет передаточную функцию
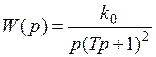 ,
, 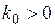 .
.
Используя критерий Попова, найти размеры сектора, которому должна принадлежать стационарная непрерывная нелинейность, при которой замкнутая САУ абсолютно устойчива.
В данном случае линейная часть САУ нейтральна, уравнение 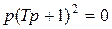 имеет один нулевой корень и два вещественных отрицательных.
имеет один нулевой корень и два вещественных отрицательных.
Строится преобразованная передаточная функция
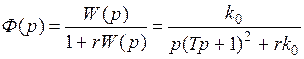 ,
,
где 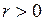 может быть сколь угодно малым;
может быть сколь угодно малым;
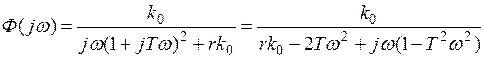 ,
,
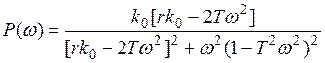 ,
,
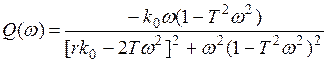 ,
,
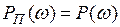 ,
, 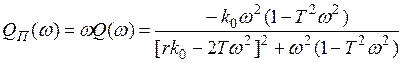 .
.
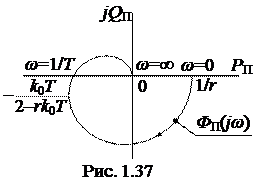 Строится преобразованная характеристика
Строится преобразованная характеристика 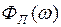
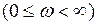 (рис.1.37), которая при
(рис.1.37), которая при 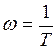 пересекает вещественную ось в точке
пересекает вещественную ось в точке 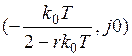 .
.
Отсюда следует, что для абсолютной устойчивости замкнутой САУ нелинейность должна удовлетворять неравенству
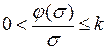 ,
,
где 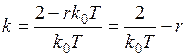 .
.
См. литературу: [2, с. 43-71; 3, с. 512-537; 10, с. 34-40].
1. Что такое устойчивость “в малом”, “в большом”, “в целом”?
2. Приведите теорему об асимптотической устойчивости.
3. Приведите теорему об экспоненциальной устойчивости.
4. Дайте определение абсолютной устойчивости.
5. Приведите частотный критерий абсолютной устойчивости Попова. Дайте геометрическую интерпретацию.
6. Каким условиям должна удовлетворять нелинейность в случае, когда линейная часть системы нейтральна или неустойчива?
7. Как можно сравнить критерий Найквиста с критерием Попова?
 2015-07-04
2015-07-04 4664
4664