Пусть движение нелинейной системы описывается нелинейными дифференциальными уравнениями второго порядка
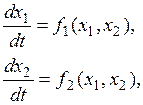 (1.1)
(1.1)
где время 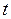 в явном виде не входит. Точки плоскости
в явном виде не входит. Точки плоскости 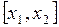 , где правые части уравнений (1.1) обращаются в ноль, т.е.
, где правые части уравнений (1.1) обращаются в ноль, т.е. 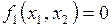 ,
, 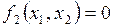 , называются особыми точками. Координаты
, называются особыми точками. Координаты 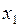 и
и 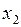 называются фазовыми координатами, каждому моменту времени
называются фазовыми координатами, каждому моменту времени 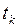 соответствует значение координат
соответствует значение координат 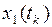 ,
, 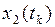 , изображаемое на фазовой плоскости
, изображаемое на фазовой плоскости 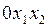 точкой (изображающая точка). Движение изображающей точки по фазовой плоскости прочерчивает линию, называемую фазовой траекторией. Наиболее распространен способ изображения, при котором используются две фазовые переменные:
точкой (изображающая точка). Движение изображающей точки по фазовой плоскости прочерчивает линию, называемую фазовой траекторией. Наиболее распространен способ изображения, при котором используются две фазовые переменные:
координатa 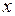 и скорость ее изменения
и скорость ее изменения 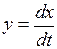 .
.
Уравнения (1.1) при этом принимают вид
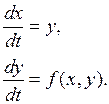 (1.2)
(1.2)
Поделив второе уравнение на первое, получим дифференциальное уравнение интегральной кривой на фазовой плоскости
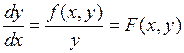 . (1.3)
. (1.3)
Решение этого уравнения дает уравнение кривых, совпадающих с фазовыми траекториями (фазовым портретом).
Фазовые траектории для системы в виде (1.2) имеют следующие особенности:
1°. Если функция 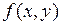 определена и непрерывна, имеет непрерывные частные производные по своим аргументам, то через любую точку фазовой плоскости, за исключением состояний равновесия (особых точек), в которых
определена и непрерывна, имеет непрерывные частные производные по своим аргументам, то через любую точку фазовой плоскости, за исключением состояний равновесия (особых точек), в которых 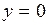 ,
, 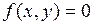 , проходит единственная интегральная кривая, т.е. фазовые траектории не пересекаются в неособых точках
, проходит единственная интегральная кривая, т.е. фазовые траектории не пересекаются в неособых точках
 2°. В верхней полуплоскости
2°. В верхней полуплоскости 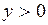 изображающая точка движется по фазовой траектории слева направо, так как координата
изображающая точка движется по фазовой траектории слева направо, так как координата 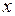 может только возрастать. При
может только возрастать. При 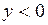 движение происходит справа налево (рис. 1.10).
движение происходит справа налево (рис. 1.10).
3°. В точках 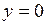 ,
, 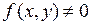 фазовые траектории пересекают ось абсцисс под прямым углом, поскольку для касательной к фазовой траектории в этих точках
фазовые траектории пересекают ось абсцисс под прямым углом, поскольку для касательной к фазовой траектории в этих точках 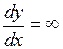 .
.
Метод фазовой плоскости кратко изложен в учебном пособии [10], где приведена классификация особых точек линейных (линеаризованных) систем.
1.3. Метод припасовывания.
Метод “припасовывания” (или “сшивания”) граничных условий представляет собой точный метод построения фазовых портретов в кусочно-линейных системах. При этом фазовая плоскость делится на области, в каждой из которых уравнения (1.2) обращаются в линейные. В каждой из выделенных областей соответствующие уравнения интегрируются, выписываются решения, строятся фазовые траектории в каждой области, которые “сшиваются” на линиях, разделяющих эти области (“ линиях переключения ”) так, что конечные значения переменных в предыдущей области являются начальными значениями этих же переменных в последующей области.
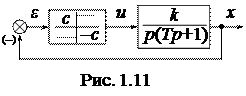 Пример 1.1. Используем метод припасовывания для построения фазового портрета нелинейной САУ типа, изображенной на рис. 1.11, где линейная часть является линеаризованной моделью электродвигателя постоянного тока с независимым возбуждением, а нелинейное звено моделирует релейный усилитель.
Пример 1.1. Используем метод припасовывания для построения фазового портрета нелинейной САУ типа, изображенной на рис. 1.11, где линейная часть является линеаризованной моделью электродвигателя постоянного тока с независимым возбуждением, а нелинейное звено моделирует релейный усилитель.
Соответствующие дифференциальные уравнения замкнутой САУ запишутся в следующем виде
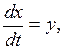
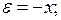 (1.4)
(1.4)
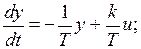
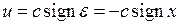 .
.
Фазовая плоскость делится на две области:
Область I: 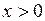 ,
, 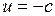 ; дифференциальные уравнения:
; дифференциальные уравнения:
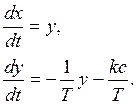 (1.5)
(1.5)
Область II: 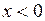 ,
, 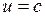 ; дифференциальные уравнения:
; дифференциальные уравнения:
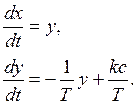 (1.6)
(1.6)
Линия переключения: 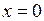 .
.
Проведем построение фазовых траекторий в области I:
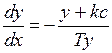 , откуда
, откуда 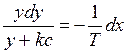 .
.
Интегрируем это уравнение при начальных условиях 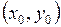
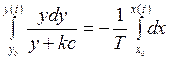 .
.
Сделаем замену 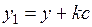 ,
, 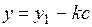 , в соответствии с которой
, в соответствии с которой
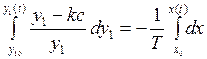 ;
;
проинтегрировав, получаем:
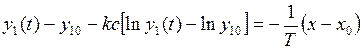 .
.
Окончательно получаем уравнение
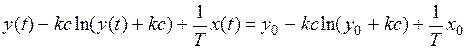 , (1.7)
, (1.7)
которому соответствует семейство фазовых траекторий (рис. 1.12), где 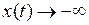 при
при 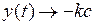 . При этом величина участка
. При этом величина участка 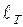 больше величины участка
больше величины участка 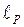 , что следует из уравнения (1.7). Действительно, при
, что следует из уравнения (1.7). Действительно, при 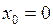 ,
,  ,
, 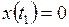 ,
, 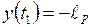 имеем
имеем 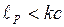 .
.
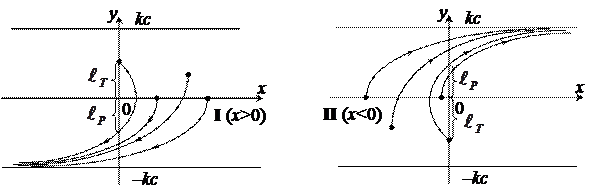 |
Рис.1.12 Рис. 1.13
Для области II соответственно получаем уравнение
|
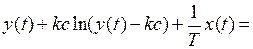
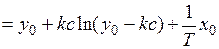 (1.8)
(1.8)
и следующее семейство фазовых траекторий, приведенное на рис. 1.13.
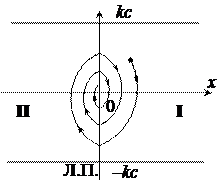
Сшивая фазовые траектории на линии переключения 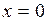 , получаем фазовый портрет (рис.1.14). Рис. 1.14
, получаем фазовый портрет (рис.1.14). Рис. 1.14
Решим далее эту же задачу для случая нелинейности типа “реле с зоной нечувствительности”. Учитывая, что 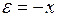 , получим:
, получим:
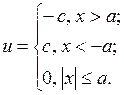
На фазовой плоскости выделяем три области:
область I: 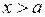 ,
, 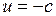 ,
,
область II: 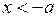 ,
, 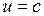 ,
,
область III: 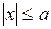 ,
, 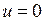 .
.
Уравнения замкнутой САУ в областях I и II совпадают с уравнениями для предыдущего случая (“идеальное реле”).
В области III получаем уравнение
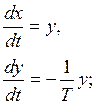 (1.9)
(1.9)
для которого
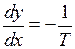 ,
, 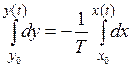 ;
;
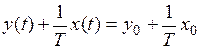 , (1.10)
, (1.10)
что соответствует фазовым траекториям в виде прямых.
Сшивая фазовые траектории по линиям переключения 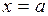 ,
, 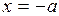 , строим фазовый портрет нелинейной САУ (рис.1.15).
, строим фазовый портрет нелинейной САУ (рис.1.15).
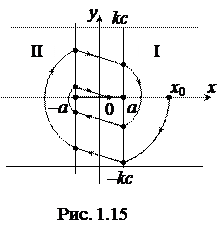 При попадании изображающей точки на отрезок покоя
При попадании изображающей точки на отрезок покоя 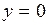 ,
, 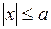 движение в САУ прекращается.
движение в САУ прекращается.
Подобным образом можно строить фазовые портреты с другими типовыми нелинейностями, приведенными на рис. 1.1-1.8.
См. литературу: [2, с.9-19; 3, с.481-489; 4, с.13-38; 5, с.414-420; 10, с.48-53].
1. Что такое фазовая плоскость?
2. Какие переменные удобно использовать для построения фазовых траекторий?
3. Как делится фазовая плоскость на области при применении метода припасовывания?
4. Как выбираются начальные условия в выделенных областях, при применении метода припасовывания?
1.4. Метод гармонической линеаризации
Это приближенный метод исследования периодических движений (автоколебаний) в нелинейных САУ, состоящих из нелинейного элемента и линейной части (рис. 1.16).
 Нелинейный элемент описывается уравнением
Нелинейный элемент описывается уравнением 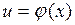 и может являться типовой нелинейностью, приведенной на рис. 1.2-1.8.
и может являться типовой нелинейностью, приведенной на рис. 1.2-1.8.
Линейная часть САУ описывается передаточной функцией
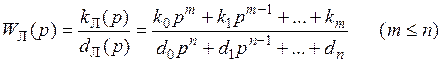 . (1.11)
. (1.11)
В таких НСАУ, при  могут возникать устойчивые периодические движения (автоколебания) на выходе линейной части, которые близки к синусоидальным, т.е.
могут возникать устойчивые периодические движения (автоколебания) на выходе линейной части, которые близки к синусоидальным, т.е. 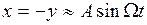 , где
, где 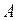 – амплитуда,
– амплитуда, 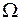 – частота автоколебаний (параметры автоколебаний). Такой динамический процесс объясняется тем, что линейная часть обладает свойством низкочастотного фильтра, пропускающего без ослабления первую (основную) гармонику и существенно ослабляющего высшие гармонические составляющие.
– частота автоколебаний (параметры автоколебаний). Такой динамический процесс объясняется тем, что линейная часть обладает свойством низкочастотного фильтра, пропускающего без ослабления первую (основную) гармонику и существенно ослабляющего высшие гармонические составляющие.
“ Гипотеза фильтра ”, принимаемая по отношению к НСАУ, лежит в основе рассматриваемого метода гармонической линеаризации. Условие низкочастотного фильтра можно записать в виде неравенства
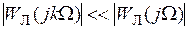 (1.12)
(1.12)
для значений  , что соответствует значительному ослаблению высших гармоник.
, что соответствует значительному ослаблению высших гармоник.
Пусть входной сигнал в НСАУ отсутствует, т.е. 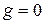 . На вход нелинейного элемента поступает сигнал
. На вход нелинейного элемента поступает сигнал 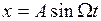 . Сигнал на выходе нелинейного элемента, являющийся периодической функцией, разложим в ряд Фурье
. Сигнал на выходе нелинейного элемента, являющийся периодической функцией, разложим в ряд Фурье
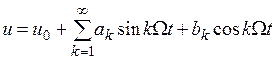 , (1.13)
, (1.13)
где
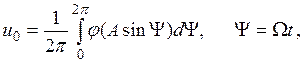
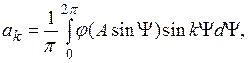 (1.14)
(1.14)
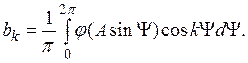
Для симметричных автоколебаний постоянная составляющая отсутствует, т.е. 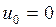 , что имеет место при симметричных нелинейных характеристиках, проходящих через начало координат (например на рис. 1.1-1.3, 1.5, 1.6).
, что имеет место при симметричных нелинейных характеристиках, проходящих через начало координат (например на рис. 1.1-1.3, 1.5, 1.6).
Рассматривая далее только симметричные автоколебаний и пренебрегая в (1.13) высшими гармониками, получим приближенное выражение
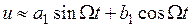 .
.
Если нелинейности описываются однозначными нечетными функциями, то 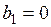 .
.
Введя обозначения
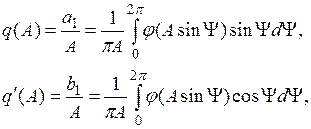 (1.15)
(1.15)
при учете, что
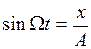 ,
, 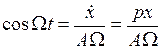 ,
,
окончательно получим из (1.15)
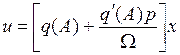 , (1.16)
, (1.16)
где 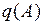 ,
, 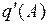 – коэффициенты гармонической линеаризации.
– коэффициенты гармонической линеаризации.
 2015-07-04
2015-07-04 2916
2916
