2015-07-04
570
Рассмотрим теперь ситуацию, когда к узкополосному шуму добавлен узкополосный же детерминированный сигнал. Комплексный случайный процесс в данном случае будет иметь следующий вид:
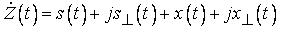
Совместная плотность вероятности вещественной и мнимой частей этого комплексного процесса будет отличаться от (2) наличием смещений для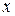 
и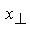 
, равных 
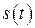и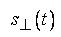 
, соответственно:
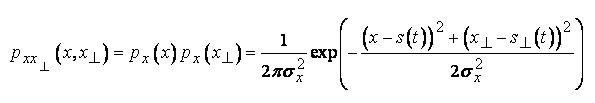
Переход от декартовой системы координат к полярной, аналогичный рассмотренному ранее (3), дает следующее:
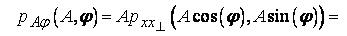
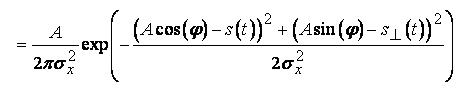
Интегрирование этой двумерной плотности по фазе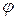 
дает одномерную плотность вероятности для амплитуды данного случайного процесса (промежуточные выкладки опущены):
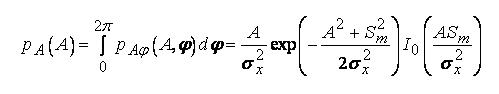
где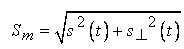 
- амплитудная огибающая детерминированного сигнала в данный момент времени.
Плотность вероятности носит название закона распределения Рэлея-Райса.
.
