2015-07-04
477
Пусть на плоскости введена аффинная система координат − (О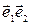 
), а М – произвольная точка пространства.
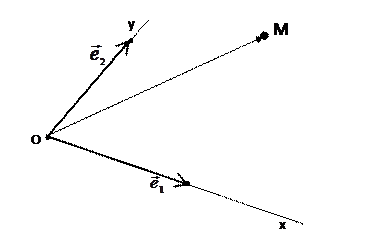
Рис.3
Определение. Вектор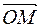 
называется радиус-вектором точки М.
Система векторов ,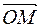 
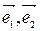является линейно зависимой. Это означает, что вектор 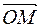можно представить в виде: 
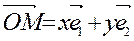. (1)
Определение. Коэффициентыx и y в разложении вектора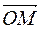 
по векторамбазиса 
данной системы координат называются координатами точки М в системе координат R= (О ).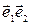
Число х называется абсциссой точки М, у – ординатой точки М. Записывается это следующим образом: М(x,y).
Другими словами, координатами точки М в системе (О 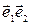) называются координаты её радиус−вектора 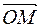в базисе данного репера R=(О, 
).
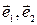Для построения т. М(x,y,z) по её координатам в системе координат (О,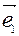 
, 
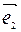) воспользуемся формулой (1). От начала координат О отложим вектор 
= =x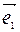 
, затем от т.М1 отложим вектор 
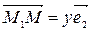. (рис.4)
Рис.4
По правилу треугольника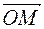 
= 
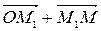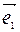= x + y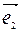 
. Таким образом, М – искомая точка. Ломаную 
называют координатной ломанной т. М. Итак, для построения точки М достаточно построить её координатную ломанную. Каждое звено имеет длину, равную 
соответствующей координате, если единицей измерения является длина соответствующего базисного вектора.
