В ходе анализа различных экономических процессов очень часто используется понятие эластичности функции, которое тесно связано с понятием производная функции.
Производная функции f(x) по аргументу x называют предел отношения приращения функции к приращению аргумента, в случае, когда приращение аргумента стремится к нулю:
Точно также как и производная функции, эластичность функции позволяет определить скорость роста функции в данной точке, но при этом значение эластичности не зависит от выбора единиц измерения как функции, так и ее аргументов (что важно для решения экономических задач)
Эластичность функции f(x) по аргументу х (обозначается 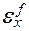 ) называют придел отношения относительного приращения функции в данной точке к относительному приращению аргумента в том случае когда относительное приращение аргумента стремится к нулю.
) называют придел отношения относительного приращения функции в данной точке к относительному приращению аргумента в том случае когда относительное приращение аргумента стремится к нулю.
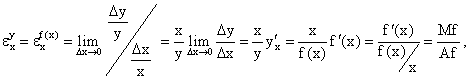
где Mf = f’(x) - предельное значение функции в данной точке, Af = f(x)/x - среднее значение функции в данной точке.
Эластичность позволяет нам оценить на сколько процентов изменит свое значение функция при изменении значения аргумента на один процент.
|
|
|
Рассмотрим основные свойства эластичности функции:
1. Эластичность функции представляет собой безразмерную величину (это непосредственно следует из определения).
2. Эластичности двух взаимно обратных функций представляют собой обратные величины.
f(x), 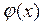 обратные, если f(
обратные, если f(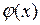 )=x.
)=x.
Доказательство:
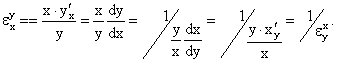
3. Эластичность произведения двух функций равна сумме эластичностей этих функций. Доказательство: пусть имеются две функции f(x) и g(x). Тогда:
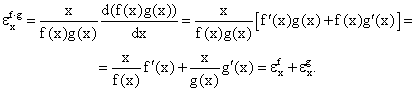
4. Эластичность частного двух функций равна эластичности числителя минус эластичность знаменателя. Доказательство: пусть имеются две функции f(x) и g(x). Тогда:

5. Эластичность суммы двух функций вычисляется по формуле:

Пример
Определим эластичность функции 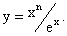 Из свойства 4 следует что эластичность нашей функции будет равна разности эластичностей числителя и знаменателя. Обозначим f(x)=xn и g(x) = ex. Имеем:
Из свойства 4 следует что эластичность нашей функции будет равна разности эластичностей числителя и знаменателя. Обозначим f(x)=xn и g(x) = ex. Имеем:
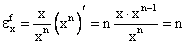 ,
, 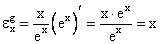 .
.
В итоге, получаем:
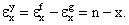
 2015-07-03
2015-07-03 2348
2348
