Тема 7. Моделирование и производственные функции

Производственная функция (функция производства) представляет уравнение, связывающее переменные величины затрат (ресурсов, факторов производства) с величиной выпуска продукции.

В экономическом моделировании наиболее широко представлены макроэкономические производственные функции. Эти функции являются агрегатными производственными функциями, характеризующими зависимость показателя совокупного общественного продукта или иного обобщающего показателя от основных факторов производства.

Производственные функции применяются для анализа влияния различных сочетаний факторов на объем выпуска и решения прогнозных и плановых задач в следующих случаях:

· для анализа влияния различных сочетаний факторов на объем выпуска в определенный момент времени (статический вариант);

· для анализа и прогнозирования соотношения объемов факторов и объемов выпуска в разные моменты времени (динамический вариант).

Так применительно к отдельной фирме производственная функция описывает максимальный объем выпуска продукции, которую эта фирма в состоянии произвести при каждом сочетании используемых факторов производства.

Для отрасли, выпускающей однородный продукт, часто рассматриваются многофакторные производственные функции, связывающие объем валового выпуска (измеренного в натуральных единицах) с затратами:

· рабочего времени по различным видам трудовой деятельности;

· различных видов сырья, энергии, полуфабрикатов, комплектующих изделий (измеренных, как и выпуск, в натуральных единицах).

При построении производственных функций крупных отраслей, регионов или народного хозяйства обычно пользуются стоимостными измерителями (как правило, в постоянных ценах), а выпуск измеряют конечным (а не валовым) продуктом. Кроме того, в этих функциях исключают или сводят к минимуму учет текущих затрат, а также включают небольшое количество переменных (по сравнению с микроэкономическим уровнем). Макроэкономические производственные функции, как правило, содержат 2-4 фактора производства, например, живой труд, основные средства, научно-технический прогресс, обобщающий показатель вовлекаемых природных ресурсов.

Частными случаями производственной функции являются:

· функция издержек, описывающая связь между объемом выпуска издержками производства;

· инвестиционная функция, описывающая зависимость необходимых инвестиций от производственной мощности будущего предприятия.

Формально производственная функция может быть записана следующим образом:

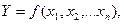
где Y – выпуск;

х_j – объем j -го ресурса.

Предполагается, что функция f(x) удовлетворяет некоторым условиям, вытекающим из общеэкономических соображений. Числовые значения параметров находятся в результате обработки, имеющейся в распоряжении исследователя информации. Это могут быть результаты пространственных выборок или временные ряды. Параметры функции оцениваются, в основном, методами корреляционно-регрессионного анализа.

Свойства, которыми должна обладать производственная функция (не всеми, но хотя бы частью):

· Выпуск невозможен при отсутствии ресурсов;

· При увеличении затрат всех ресурсов выпуск также растет;

· При увеличении затрат любого из ресурсов, при неизменном количестве остальных, выпуск не сокращается;

· С увеличением затрат любого из ресурсов, при неизменном количестве остальных, эффективность вовлечения в производство дополнительной его единицы не возрастает (принцип убывающей отдачи последовательных вложений);

· Эффективность затрат любого из ресурсов при увеличении затрат какого-либо другого ресурса и неизменном количестве остальных, не снижается;

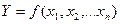· − строго квазивогнута;

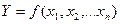· − строго вогнута (выпукла вверх).

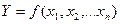· однородна степени 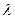, т. е. 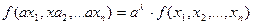, при 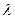>1 с увеличением масштабов производства его эффективность растет (растущая отдача или экономия от масштаба), при 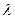< 1 − падает (падающая отдача или потери от масштаба), при 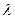=1 – не меняется. В одних случаях значение 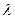оценивается статистически, в других на него накладываются априорные ограничения. В подавляющем большинстве малоразмерных моделей экономического роста предполагается, что 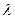= 1.

Нужно помнить, что не все производственные функции и не при всех значениях входящих в них переменных обладают перечисленными свойствами. Иногда требуется, чтобы производственная функция обладала дополнительными свойствами.

С помощью производственной функции рассчитывают следующие характеристики:

· предельная производительность (отражает насколько увеличивается выпуск при увеличении затрат фактора j на одну единицу, при неизменном количестве остальных факторов);

· частная эластичность выпуска по фактору j (отражает насколько процентов увеличится выпуск при увеличении затрат фактора j на 1% и при неизменном количестве остальных факторов);

· эластичность производства (показывает, на сколько процентов увеличится выпуск при увеличении на 1% затрат каждого фактора);

· предельная норма замены (замещения) фактора j фактором i (этот показатель определяет количество фактора j, которое требует требуется для замены одной единицы фактора j при сохранении на неизменном уровне объема выпуска и количества остальных факторов;

· эластичность замены (замещения) фактора j фактором i (показатель характеризует возможность замены одного фактора другим).

Таким образом, с помощью производственных функций изучается взаимозаменяемость факторов производства, которая может быть неизменной либо переменной (т. е. зависимой от объемов ресурсов).

Соответственно, функции делят на два вида:

· с постоянной эластичностью замены (CES − Constant Elasticity of Substitution);

· с переменной эластичностью замены (VES − Variable Elasticity of Substitution).

Далее рассмотрим основные формы представления производственной функции.

Линейная: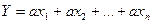

Леонтьевская: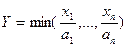

Кобба-Дугласа: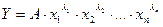

С постоянной эластичностью замещения: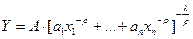

Наиболее популярной и в теоретических, и в прикладных исследованиях является функция Кобба-Дугласа: она сочетает простоту математической записи, очевидную экономическую интерпретацию и относительную легкость определения численных значений ее параметров. Особенность этой мультипликативно-степенной формы производственной функции состоит в том, что если один из сомножителей равен нулю, то результат обращается также в нуль. Это свойство соответствует тому факту, что в большинстве случаев для производства необходимы все факторы и при отсутствии одного из них выпуск продукции невозможен.

Функция Кобба-Дугласа может быть записана в канонической форме: .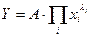

Коэффициент А учитывает размерность, которая, в свою очередь, зависит от выбранной единицы измерений затрат и выпуска. В качестве результативного показателя можно принять объем конечного продукта, а в качестве сомножителей – основные факторы производства:

· численность занятого населения х₁;

· величину основного и оборотного капитала х₂;

· площадь используемой земли х₃.

С помощью функции Кобба-Дугласа была сделана попытка оценить связь таких факторов, как труд и капитал, с ростом национального дохода США в 20-30 годов XX века:

,

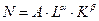где N − национальный доход;

А − коэффициент размерности;

L и К − соответственно объемы приложенного труда и капитала;

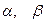− коэффициенты эластичности производства по труду L и капиталу К.

Функция Кобба-Дугласа используется для описания объема производства в зависимости от числа занятых (наряду с капиталом):

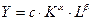
где Y − объем производства;

К − величина капитала;

L − численность занятых;

с − постоянный параметр производительности;

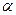− коэффициент эластичности производства по отношению к величине

капитала;

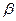− коэффициент эластичности производства по отношению к численности

занятых.

Сумма коэффициентов эластичности характеризует эффект масштаба производства:

· возрастающий, если 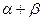> 1;

· постоянный, если 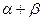=1;

· убывающий, если 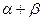< 1.

Хотя сумма 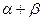может принимать любые значения, чаще всего предполагается неизменный масштаб производства. В связи с этим предположением, один параметр определяется через другой: 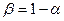. В «классической» производственной функции Кобба-Дугласа 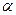= 0,33, 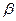= 0,67.

Среди моделей, характеризующих влияние демографического фактора на экономическое развитие, выделяются динамические модели, основанные на предположении, что технологические изменения влияют на объем производства непосредственно (модель Р. Солоу):

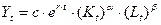
где t − календарный год;

r − постоянный темп технического развития.

Модель М. Брауна также учитывает техническое развитие:

.

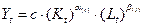Еще одна модель Солоу учитывает качественные изменения внутри факторов производства:

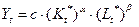
где индекс * отражает качественные изменения в физическом или человеческом капитале.

В динамическом варианте применяются разные формы производственной функции. Например, в двухфакторном случае:

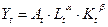
где множитель A_t – обычно возрастает во времени, отражая общий рост эффективности факторов производства в динамике.

Важнейшей проблемой использования производственных функций является учет в них фактора технического прогресса.

Моделирование научно-технического прогресса развивается

в двух направлениях:

· анализ динамики сквозных агрегатных показателей, измеряющих экономический рост;

· изучение процессов появления и распространения нововведений.

Производственные функции явялются средством адекватного представления роли технического прогресса и способов его измерения. Интерпретировать результаты развития экономики было удобнее в емповых характеристиках. Если переменные производственной функции типа Кобба-Дугласа: 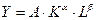считать зависящими от времени, то ее легко преобразовать в линейное соотношение между темпами прироста:

где 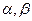− темпы прироста.

За счет учета «остатка» (часть экономического роста, которую нельзя объяснить традиционно рассматриваемыми экономическими факторами, т.е. рост за счет НТП), функция приобрела вид:

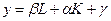
Производственная функция, для которой 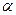= 0,25, 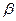= 0,75, интерпретируется следующим образом:

· увеличение на 1% основных фондов (основного капитала) ведет к приросту (при фиксированной численности занятых) на 0,25%;

· увеличение на 1% численности занятых вызывает соответственно прирост выпуска на 0,75%.

Это так называемые экстенсивные факторы роста. Кроме того, наблюдается прирост выпуска на 2% в среднем за год за счет всех остальных факторов, совместное влияние которых относят за счет результирующего технического прогресса (интенсивные, факторы роста).

Если в среднем за период К=3%, L=1%, то 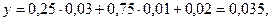то есть выпуск будет увеличиваться на 3,5% в год. Чтобы определить вклад «технического прогресса» в экономический рост, рассчитывают величину 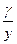. В данном случае этот вклад объясняет 57% прироста, т.е. на долю интенсивных факторов относят 57% прироста выпуска, а на долю экстенсивных – 43%.

Известны многочисленные попытки усовершенствовать модельные представления о техническом прогрессе, порождаемые производственными

функциями. В частности, введение в модель параметра «срок службы основного капитала» позволило отразить зависимость производительности основных фондов от времени, учесть не только физический, но и моральный износ оборудования. Предпринимались попытки моделирования роста квалификации вновь вовлекаемых в производство трудовых ресурсов и влияния своевременной

переподготовки работающих.