Симметричность

Определение.

Пусть 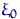, , 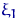, 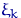независимы и имеют стандартное нормальное распределение. Распределение случайной величины

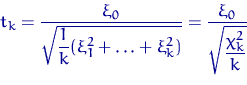
называют распределением Стьюдента с 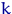степенями свободы и обозначают .

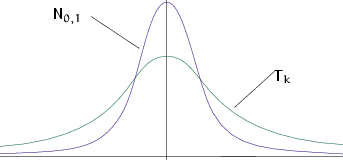
Плотность распределения Стьюдента по сравнению с плотностью стандартного нормального распределения.

Свойства распределения Стьюдента:

1.

Симметричность.

Если случайная величина 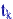имеет распределение Стьюдента с 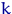степенями свободы, то и 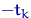имеет такое же распределение. (Сразу следует из определения).

2. Mt_k=0; D 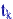= k/(k-2), k>2.

Отметим, что и распределение 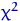, и распределение Стьюдента табулированы, так что если в каких-то доверительных интервалах появятся квантили этих распределений, то мы найдем их по таблице.

Следующее распределение тоже тесно связано с нормальным распределением, но понадобится нам не при построения доверительных интервалов, а чуть позже — в задачах проверки гипотез

$4. Распределение Фишера