Определение. Иррациональным уравнением называют уравнение, в котором переменная содержится под знаком радикала или возведена в дробную степень.
К простейшим иррациональным уравнениям относят уравнения вида: 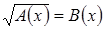 ,
, 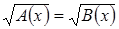 , где
, где 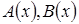 – выражения с переменной.
– выражения с переменной.
Основная идея решения иррационального уравнения состоит в сведении его к рациональному алгебраическому уравнению, которое либо равносильно исходному иррациональному уравнению, либо является его следствием.
Главный способ избавиться от корня и получить рациональное уравнение – возведение обеих частей уравнения в одну и ту же степень, которую имеет корень, содержащий неизвестное, и последующее «освобождение» от радикалов по формуле 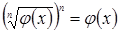 .
.
Если обе части иррационального уравнения возвести в одну и ту же нечетную степень и освободиться от радикалов, то получится уравнение, равносильное исходному уравнению.
При возведении уравнения в четную степень получают уравнение, являющееся следствием исходного. Поэтому возможно появление посторонних решений уравнения. Причина приобретения корней состоит в том, что при возведении в четную степень чисел, равных по абсолютной величине, но разных по знаку, получается один и тот же результат.
Заметим, что потеря корней при возведении уравнения в четную степень невозможна.
Так как могут появиться посторонние корни, то необходимо делать проверку, подставляя найденные значения неизвестной только в первоначальное уравнение.
Рассмотрим применение данного метода для решения иррациональных уравнений вида: 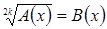 .
.
Пример. Решим уравнение: 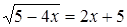 .
.
Решение. Возведем обе части этого уравнения в квадрат: 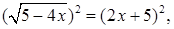 получим
получим 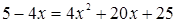
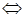
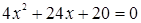
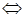
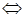
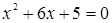 , откуда следует, что
, откуда следует, что 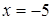 или
или 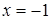 .
.
Проверка. 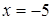 :
: 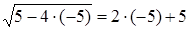
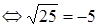 . Это неверное числовое равенство, следовательно, число
. Это неверное числовое равенство, следовательно, число 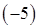 не является корнем данного уравнения.
не является корнем данного уравнения.
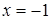 :
: 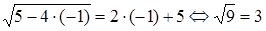 . Это верное числовое равенство, следовательно,, число
. Это верное числовое равенство, следовательно,, число 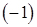 является корнем данного уравнения.
является корнем данного уравнения.
Ответ. 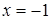 .
.
Пример. Решим уравнение: 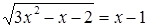 .
.
Решение. После возведения в квадрат получаем уравнение: 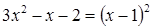
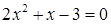 , откуда следует, что
, откуда следует, что 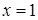 или
или 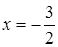 .
.
Проверка. 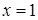 :
: 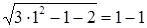
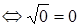 . Это верное числовое равенство, следовательно,, число
. Это верное числовое равенство, следовательно,, число 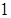 является корнем данного уравнения.
является корнем данного уравнения.
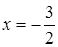 :
: 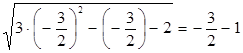
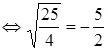 . Это неверное числовое равенство, следовательно,, число
. Это неверное числовое равенство, следовательно,, число 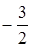 не является корнем данного уравнения.
не является корнем данного уравнения.
Ответ. 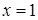 .
.
Пример. Решим уравнение: 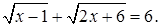
Решение. Преобразуем уравнение к виду: 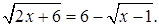 Возведем обе части данного уравнения в квадрат, получим:
Возведем обе части данного уравнения в квадрат, получим: 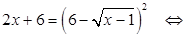
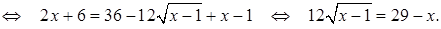
Еще раз возведем обе части уравнения в квадрат, имеем:
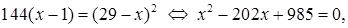 откуда х 1=5; х 2=197.
откуда х 1=5; х 2=197.
Проверка показывает, что х 2=197 – посторонний корень, х =5 – корень уравнения.
Ответ. 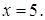
Метод сведения к эквивалентной системе уравнений и неравенств
Проверка, осуществляемая подстановкой найденного решения в исходное уравнение, может быть легко реализована, если проверяемые корни – «хорошие» числа, для «громоздких» корней проверка может быть сопряжена со следовательно,ельными вычислительными трудностями. Поэтому иногда более рационально решать иррациональные уравнения с помощью равносильных преобразований, так как, выполняя равносильные преобразования, можно не опасаться ни потери корней, ни приобретения посторонних решений.
Аккуратное возведение в четную степень уравнения вида 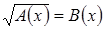 состоит в переходе к одной из равносильных ему систем:
состоит в переходе к одной из равносильных ему систем:
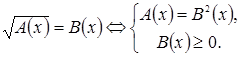
Неравенство 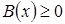 в этой системе выражает условие, при котором уравнение можно возводить в четную степень, отсекает посторонние решения и позволяет обходиться без проверки.
в этой системе выражает условие, при котором уравнение можно возводить в четную степень, отсекает посторонние решения и позволяет обходиться без проверки.
Иногда добавляют к данной системе неравенство 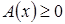 . Однако этого делать не нужно и даже опасно, поскольку условие
. Однако этого делать не нужно и даже опасно, поскольку условие 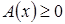 автоматически выполняется для корней уравнения
автоматически выполняется для корней уравнения 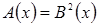 , в правой части которого стоит неотрицательное выражение.
, в правой части которого стоит неотрицательное выражение.
Пример. Решим уравнение: 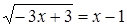 .
.
Решение. Это уравнение равносильно системе: 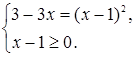
Решим первое уравнение системы, оно равносильно уравнению 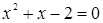 , получим корни
, получим корни 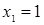 и
и 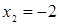 .
.
Второй корень не удовлетворяет неравенству системы и, следовательно, является посторонним корнем исходного уравнения.
Ответ. 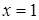 .
.
Рассмотрим схему решения еще одного вида иррациональных уравнений 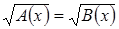 .
.
Такое уравнение равносильно каждой из двух систем:
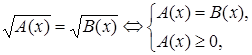 или
или 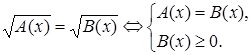
Поскольку после возведения в четную степень получают уравнение, являющееся следствием уравнения 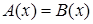 , то решив его, необходимо выяснить, принадлежат ли найденные корни области определения исходного уравнения, то есть выполняется ли неравенство
, то решив его, необходимо выяснить, принадлежат ли найденные корни области определения исходного уравнения, то есть выполняется ли неравенство 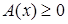 (или
(или 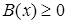 ).
).
На практике из этих систем выбирают для решения ту, в которой неравенство проще.
Пример. Решим уравнение: 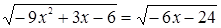 .
.
Решение. Это уравнение равносильно системе: 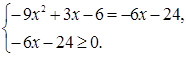
Решим первое уравнение системы, оно равносильно уравнению 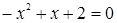 , получим корни
, получим корни 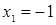 и
и 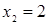 .
.
Однако, при этих значениях x не выполняется неравенство 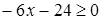 , и потому данное уравнение не имеет корней.
, и потому данное уравнение не имеет корней.
Ответ. Корней нет.
Пример. Решим уравнение: 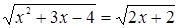 .
.
Решение. Данное уравнение равносильно системе:
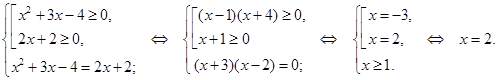
Ответ 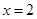 .
.
Пример. Решим уравнение: 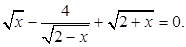
Решение. Умножим данное уравнение на 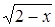 , тогда исходное уравнение равносильно системе:
, тогда исходное уравнение равносильно системе:
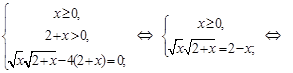
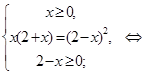
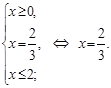
Ответ. 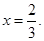
Метод уединения радикала
При решении иррациональных уравнений иногда целесообразно перед возведением обеих частей уравнения в некоторую степень «уединить радикал», то есть представить уравнение в виде 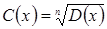 . После возведения обеих частей уравнения в n- ую степень радикал в правой части равенства исчезнет.
. После возведения обеих частей уравнения в n- ую степень радикал в правой части равенства исчезнет.
Пример. Решим уравнение: 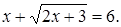
Решение. Метод уединения радикала приводит к уравнению 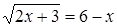 . Данное уравнение равносильно системе:
. Данное уравнение равносильно системе: 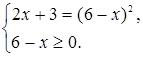
Решим уравнение 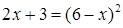 , получим корни
, получим корни 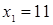 и
и 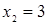 , но условие
, но условие 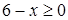 выполняется только для
выполняется только для 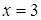 .
.
Ответ. 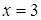 .
.
Пример. Решим уравнение: 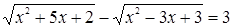 .
.
Решение. Уединив первый радикал, получаем уравнение равносильное исходному: 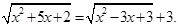
Возводя обе части этого уравнения в квадрат, получаем уравнение:
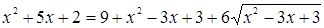
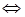
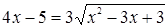 .
.
Последнее уравнение является следствием исходного уравнения.
Возводя обе части этого уравнения в квадрат, приходим к уравнению:
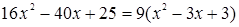
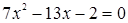 .
.
Это уравнение является следствием исходного уравнения и имеет корни 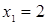 ,
, 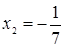 . Первый корень удовлетворяет исходному уравнению, второй корень не удовлетворяет исходному уравнению.
. Первый корень удовлетворяет исходному уравнению, второй корень не удовлетворяет исходному уравнению.
Ответ. 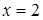 .
.
Метод введения новой переменной
Удобным средством решения иррациональных уравнений является метод введения новой переменной, или «метод замены». Метод обычно применяют в случае, если в уравнении неоднократно встречается некоторое выражение, зависящее от неизвестной величины. Обозначают такое выражение новой переменной, затем решают уравнение сначала относительно введенной переменной, затем возвращаются к исходной переменной и находят ее.
В ряде случаев удачно введенные новые переменные позволяют получить решение быстрее и проще.
Пример. Решим уравнение: 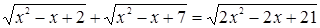 .
.
Решение. Введем новую переменную. Пусть 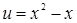 , тогда получим существенно более простое иррациональное уравнение
, тогда получим существенно более простое иррациональное уравнение 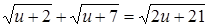
 .
.
Возведем обе части уравнения в квадрат: 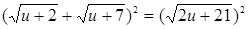 .
.
Далее последовательно получаем: 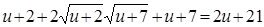 ;
; 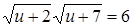 ;
; 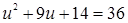 ;
; 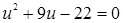 ;
; 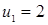 ,
, 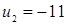 .
.
Проверяем найденные значения методом подстановки в уравнение: 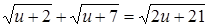 , отсюда следует, что
, отсюда следует, что 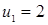 – корень уравнения, а
– корень уравнения, а 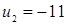 – посторонний корень.
– посторонний корень.
Вернемся к исходной переменной x, получим уравнение 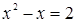 , то есть квадратное уравнение
, то есть квадратное уравнение 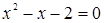 , решив которое находим два корня:
, решив которое находим два корня: 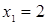 ,
, 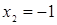 . Оба корня, как показывает проверка, удовлетворяют исходному уравнению.
. Оба корня, как показывает проверка, удовлетворяют исходному уравнению.
Ответ. 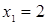 ,
, 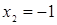 .
.
Замена особенно полезна, если в результате достигается новое качество, например, иррациональное уравнение сводится к квадратному уравнению.
Пример. Решим уравнение: 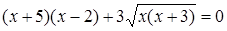 .
.
Решение. Перепишем уравнение так: 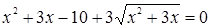 .
.
Введем новую переменную. Пусть 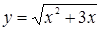 , тогда уравнение примет вид:
, тогда уравнение примет вид: 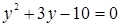 , откуда
, откуда 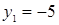 ,
, 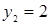 .
.
Вернемся к исходной переменной, получим два уравнения: 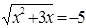 и
и 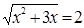 . Первое из уравнений решения не имеет, из второго уравнения получим
. Первое из уравнений решения не имеет, из второго уравнения получим 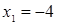 ,
, 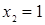 .
.
Оба корня, как показывает проверка, удовлетворяют исходному уравнению.
Ответ. 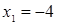 ,
, 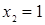 .
.
Отметим, что «бездумное» применение в данном примереметода «уединения радикала» и возведение в квадрат привело бы к уравнению четвертой степени, решение которого представляет собой в общем случае чрезвычайно сложную задачу.
Пример. Решим уравнение: 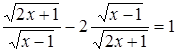 .
.
Решение. Введем новую переменную. Пусть 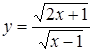 ,
, 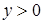 .
.
Тогда исходное иррациональное уравнение сведено к квадратному уравнению: 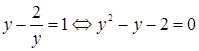 , откуда учитывая ограничение
, откуда учитывая ограничение 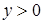 , получим
, получим 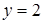 . Решим уравнение
. Решим уравнение 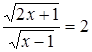 , получим корень
, получим корень 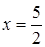 .
.
Как показывает проверка, 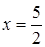 удовлетворяет исходному уравнению.
удовлетворяет исходному уравнению.
Ответ. 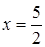 .
.
Метод сведения к эквивалентным системам рациональных уравнений
Иногда посредством некоторой подстановки удается привести иррациональное уравнение к рациональному виду.В таком случае говорят, что такая подстановка рационализирует рассматриваемое иррациональное уравнение. Метод решения, основанный на применении рационализирующих подстановок, называют методом рационализации.
Уравнения вида 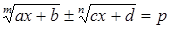 (здесь a, b, c, d – некоторые числа, m, n – натуральные числа) и ряд других уравнений часто удается решить при помощи введения двух вспомогательных неизвестных:
(здесь a, b, c, d – некоторые числа, m, n – натуральные числа) и ряд других уравнений часто удается решить при помощи введения двух вспомогательных неизвестных: 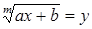 и
и 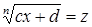 , где
, где 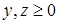 и последующего перехода к эквивалентной системе рациональных уравнений.
и последующего перехода к эквивалентной системе рациональных уравнений.
Пример. Решим уравнение: 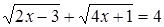 .
.
Решение. Введем новые переменные. Пусть 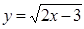 и
и 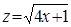 , где
, где 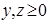 . Тогда исходное уравнение принимает вид:
. Тогда исходное уравнение принимает вид: 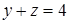 .
.
Полученное уравнение обладает одним существенным недостатком: в нем два неизвестных. Однако, величины y и z не являются независимыми переменными – они зависят одна от другой посредством исходной переменной x. Выразим x через y и z: 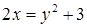 и
и 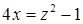 .
.
Умножим первое уравнение на два, вычтем из него второе уравнение, тогда переменная x исключена, и остается связь только между y и z: 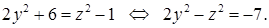
В результате получим систему двух уравнений относительно двух неизвестных y и z: 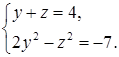
Решим систему методом подстановки, получим уравнение: 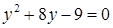 , корнями которого являются числа
, корнями которого являются числа 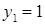 и
и 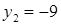 .
.
Корень 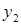 посторонний, поскольку
посторонний, поскольку 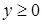 .
.
Решим уравнение 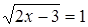 , получим
, получим 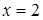 .
.
Ответ. 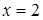 .
.
Пример. Решим уравнение: 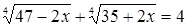 .
.
Решение. Возведение обеих частей данного уравнения в четвертую степень не обещает ничего хорошего. Если же предположить, что 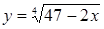 ,
, 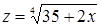 , то исходное уравнение примет вид:
, то исходное уравнение примет вид: 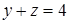 .
.
Поскольку введены две новые неизвестные, необходимо найти еще одно уравнение, связывающее y и z. Для этого возведем равенства 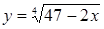 ,
, 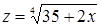 в четвертую степень и заметим, что
в четвертую степень и заметим, что 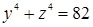 .
.
Решим систему уравнений: 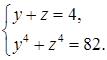
Система имеет два действительных решения: 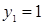 ,
, 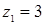 ;
; 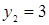 ,
, 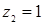 .
.
Р ешим две системы уравнений с одним неизвестным:
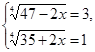 и
и 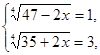
Решением первой системы является 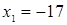 , второй
, второй 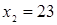 .
.
Ответ. 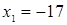 ,
, 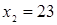 .
.
Не всегда после введения новых переменных удается исключить неизвестную x, как это было в рассмотренныхвыше примерах. Однако, можно убедиться из следующего примера, что переход от уравнения к системе может быть полезен и в таком случае.
Пример. Решим уравнение: 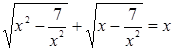 .
.
Решение. Введем новые переменные. Пусть 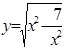 и
и 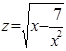 , где
, где 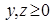 .
.
Тогда по стандартной схеме получим систему уравнений: 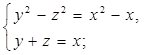
откуда следует, что 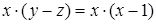 .
.
Так как 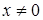 , то y и z должны удовлетворять системе:
, то y и z должны удовлетворять системе: 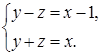
Возведем оба уравнения этой системы в квадрат, после чего, сложив их, получаем уравнение 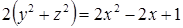 .
.
Возведем равенства 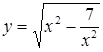 ,
, 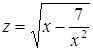 в квадрат и заметим, что
в квадрат и заметим, что 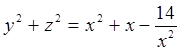 .
.
Получим систему уравнений: 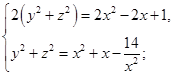
решая её, получим уравнение 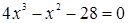 .
.
Заметим, что это уравнение имеет корень 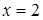 .
.
Разделим многочлен 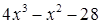 на
на 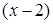 , получим разложение левой части уравнения на множители:
, получим разложение левой части уравнения на множители: 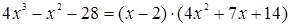 .
.
Отсюда следует, что 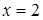 – единственное решение этого уравнения.
– единственное решение этого уравнения.
Как показывает проверка, 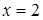 удовлетворяет исходному уравнению.
удовлетворяет исходному уравнению.
Ответ. 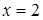 .
.
Умножение обеих частей уравнения на функцию
Иногда иррациональное уравнение удается решить довольно легко, если обе его части умножить на удачно подобранную функцию. Однако при умножении обеих частей уравнения на некоторую функцию могут появиться посторонние решения, ими могут оказаться нули данной функции. Поэтому данный метод требует обязательного исследования получившихся значений.
Пример. Решим уравнение: 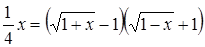 .
.
Решение. Умножим обе части уравнения на функцию 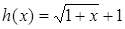 . Выражение
. Выражение 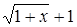 называют сопряженным для выражения
называют сопряженным для выражения 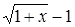 . Цель такого умножения ясна: использовать тот факт, что произведение двух сопряженных выражений уже не содержит радикалов.
. Цель такого умножения ясна: использовать тот факт, что произведение двух сопряженных выражений уже не содержит радикалов.
В результате умножения и очевидных преобразований получим уравнение:
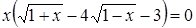 , которое равносильно совокупности уравнений:
, которое равносильно совокупности уравнений:
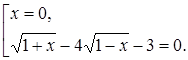
Уединив первый радикал второго уравнения совокупности, возведем его в квадрат, имеем:
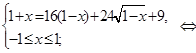
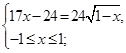
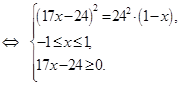
Проанализировав неравенства последней системы, можно заметить, что пересечение множеств 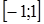 и
и 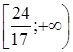 пусто. Следовательно, уравнение
пусто. Следовательно, уравнение 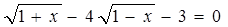 решений не имеет.
решений не имеет.
Таким образом, уравнение 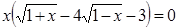 имеет единственный корень
имеет единственный корень 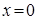 . Подстановка в его исходное уравнение показывает, что
. Подстановка в его исходное уравнение показывает, что 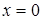 – корень уравнения.
– корень уравнения.
Заметим, что при решении данного уравнения можно было обойтись и без подстановки: функция 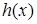 нигде в ноль не обращается, и поэтому умножение обеих частей уравнения
нигде в ноль не обращается, и поэтому умножение обеих частей уравнения 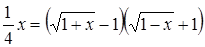 на эту функцию не приводит к появлению посторонних решений.
на эту функцию не приводит к появлению посторонних решений.
Ответ. 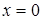 .
.
Пример. Решим уравнение: 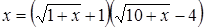 .
.
Решение. Умножим обе части уравнения на функцию 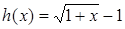 . После преобразований получим уравнение:
. После преобразований получим уравнение:  .
.
Оно имеет два корня: 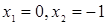 . Проверка показывает, что
. Проверка показывает, что 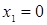 – посторонний корень. Заметим, что
– посторонний корень. Заметим, что 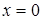 – корень функции
– корень функции 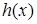 .
.
Таким образом, уравнение имеет единственный корень 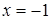 .
.
Ответ. 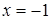 .
.
Решение иррациональных уравнений с использованием свойств, входящих в них функций
В некоторых случаях, при решении иррациональных уравнений, целесообразно применять свойства элементарных функций. Рассмотрим несколько примеров решения иррациональных уравнений с использованием свойств входящих в них функций.
Использование монотонности функции
Если уравнение имеет вид 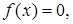 где функция
где функция 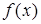 возрастает (убывает), или
возрастает (убывает), или 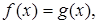 где
где 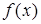 и
и 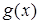 «встречно монотонны», то есть
«встречно монотонны», то есть 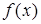 возрастает, а
возрастает, а 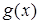 убывает, и наоборот, то такое уравнение имеет не более одного корня. Если удается привести уравнение к такому виду и при этом нетрудно подобрать корень, то он и будет решением данного уравнения.
убывает, и наоборот, то такое уравнение имеет не более одного корня. Если удается привести уравнение к такому виду и при этом нетрудно подобрать корень, то он и будет решением данного уравнения.
Пример. Решим уравнение: 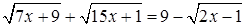 .
.
Решение. Это уравнение можно попытаться решить возведением в квадрат (трижды). Однако, в таком случае получится уравнение четвертой степени. Попробуем подобрать корень. Это сделать нетрудно: 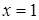 .
.
Заметим, что левая часть уравнения 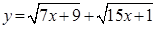 – возрастающая функция, а правая часть уравнения
– возрастающая функция, а правая часть уравнения 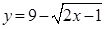 – убывающая функция. Следовательно, больше одного корня данное уравнение иметь не может.
– убывающая функция. Следовательно, больше одного корня данное уравнение иметь не может.
Таким образом, 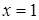 – единственный корень исходного уравнения.
– единственный корень исходного уравнения.
Ответ. 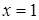 .
.
Пример. Решим уравнение: 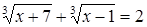 .
.
Решение. Традиционный метод решения уравнений такого вида хорошо известен. Однако, легко заметить, что 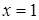 – корень. Левая часть уравнения задает возрастающую функцию, правая – константу. Следовательно, данное уравнение может иметь не более одного корня. Итак,
– корень. Левая часть уравнения задает возрастающую функцию, правая – константу. Следовательно, данное уравнение может иметь не более одного корня. Итак, 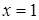 – единственный корень.
– единственный корень.
Ответ. 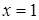 .
.
Пример. Решим уравнение: 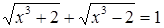 .
.
Решение. 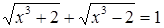 – стандартное иррациональное уравнение. Тем не менее, не будем спешить возводить в квадрат обе части уравнения. Так как,
– стандартное иррациональное уравнение. Тем не менее, не будем спешить возводить в квадрат обе части уравнения. Так как, 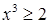 ,
, 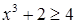 ,
, 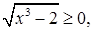 то
то 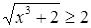 (функция
(функция 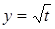 возрастающая), и левая часть исходного уравнения не меньше 2. Следовательно, данное уравнение корней не имеет.
возрастающая), и левая часть исходного уравнения не меньше 2. Следовательно, данное уравнение корней не имеет.
Ответ. Корней нет.
Пример. Решим уравнение: 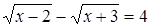 .
.
Решение. Поскольку 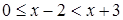 и функция
и функция 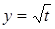 возрастающая, то
возрастающая, то 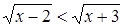 . Следовательно, левая часть данного неравенства области определения принимает только отрицательные значения, то есть исходное уравнение корней не имеет.
. Следовательно, левая часть данного неравенства области определения принимает только отрицательные значения, то есть исходное уравнение корней не имеет.
Ответ. Корней нет.
Пример. Решим уравнение: 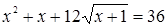 .
.
Решение. Как и в рассмотренных выше примерах, несложно обнаружить, что 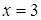 – корень уравнения. Областью определения исходного уравнения является промежуток
– корень уравнения. Областью определения исходного уравнения является промежуток 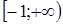 . В отличие от ранее рассмотренных задач, левая часть уравнения не задает монотонную функцию. Однако, легко заметить, что на
. В отличие от ранее рассмотренных задач, левая часть уравнения не задает монотонную функцию. Однако, легко заметить, что на 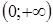 указанная функция возрастает, причем корень
указанная функция возрастает, причем корень 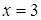 принадлежит промежутку
принадлежит промежутку 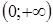 . Следовательно,, на данном промежутке уравнение
. Следовательно,, на данном промежутке уравнение 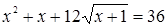 имеет единственный корень
имеет единственный корень 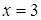 .
.
Исследуем поведение функции 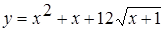 на отрезке
на отрезке 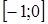 . Очевидно, что при
. Очевидно, что при 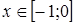
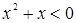 , а
, а 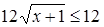 .
.
Следовательно, на 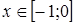 исходное уравнение корней не имеет.
исходное уравнение корней не имеет.
Ответ. 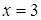 .
.
Использование области определения уравнения
Иногда знание области определения уравнения позволяет доказать, что уравнение не имеет решений, а иногда позволяет найти решения уравнения непосредственной подстановкой чисел из области определения уравнения.
Пример. Решим уравнение: 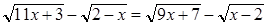 .
.
Решение. Данное иррациональное уравнение можно решить путем традиционного возведения обеих частей уравнения в квадрат. Однако, найдя область определения исходного уравнения, приходим к выводу, что область определения уравнения – одноэлементное множество {2}. Подставив 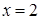 в данное уравнение, приходим к выводу, что
в данное уравнение, приходим к выводу, что 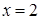 – корень исходного уравнения.
– корень исходного уравнения.
Ответ. 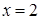 .
.
Пример. Решим уравнение: 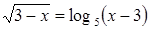 .
.
Решение. Область определения исходного уравнения состоит из всех 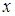 , одновременно удовлетворяющих условиям
, одновременно удовлетворяющих условиям 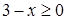 и
и 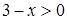 , то есть область определения исходного уравнения есть пустое множество. Этим решение уравнения завершается, так как установлено, что ни одно число не может являться решением, то есть уравнение не имеет корней.
, то есть область определения исходного уравнения есть пустое множество. Этим решение уравнения завершается, так как установлено, что ни одно число не может являться решением, то есть уравнение не имеет корней.
Ответ. Корней нет.
Использование графиков функций
При решении уравнений или неравенств иногда полезно рассмотреть эскиз графиков их правой и левой частей в одной и той же системе координат. В некоторых случаях эскиз графиков помогает выяснить, на какие множества необходимо разбить числовую ось, чтобы на каждом из них решение уравнения или неравенства было очевидно. Заметим, что эскиз графика лишь помогает найти решение, но ответ необходимо обосновать.
Пример. Решим уравнение: 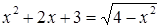 .
.
Решение. Область определения исходного уравнения есть все все значения переменой 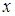 из промежутка
из промежутка 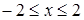 . Эскизы графиков функций
. Эскизы графиков функций 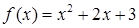 и
и 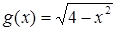 представлены на рисунке 20.
представлены на рисунке 20.
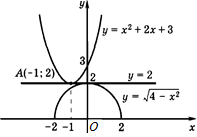
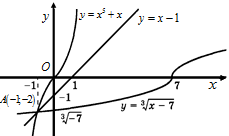
Рис.20 Рис.21
Проведем прямую 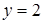 . Из рисунка 20 следует, что график функции
. Из рисунка 20 следует, что график функции 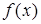 лежит не ниже этой прямой, а график функции
лежит не ниже этой прямой, а график функции 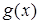 не выше. При этом эти графики касаются прямой
не выше. При этом эти графики касаются прямой 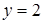 в разных точках.
в разных точках.
Следовательно, уравнение не имеет решений.
Докажем данное утверждение. Для каждого 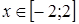 имеем
имеем 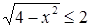 , а
, а 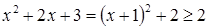 . При этом
. При этом 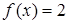 только для
только для 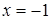 , а
, а 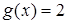 только для
только для 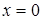 . Это означает, что исходное уравнение не имеет корней.
. Это означает, что исходное уравнение не имеет корней.
Ответ. Корней нет.
Пример. Решим уравнение: 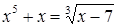 .
.
Решение. Эскизы графиков функций 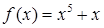 и представлены на рисунке 21. Легко проверить, что точка
и представлены на рисунке 21. Легко проверить, что точка 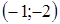 является точкой пересечения графиков функций
является точкой пересечения графиков функций 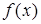 и
и 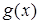 , то есть
, то есть 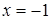 – решение уравнения.
– решение уравнения.
Проведем прямую 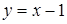 . Из рисунка 21 следует, что данная прямая расположена между графиками функций
. Из рисунка 21 следует, что данная прямая расположена между графиками функций 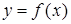 и
и 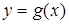 .
.
Докажем, что других решений данное уравнение не имеет.
Для этого докажем, что для 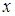 из промежутка
из промежутка 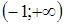 справедливы неравенства
справедливы неравенства 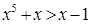 и
и 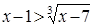 , а для промежутка
, а для промежутка 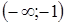 справедливы неравенства
справедливы неравенства 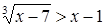 и
и 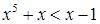 . Очевидно, что неравенство
. Очевидно, что неравенство 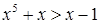 справедливо для
справедливо для 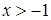 , а неравенство
, а неравенство 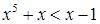 для
для 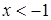 .
.
Решим неравенство 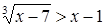 . Это неравенство равносильно неравенству
. Это неравенство равносильно неравенству 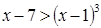 , которое можно переписать в виде
, которое можно переписать в виде 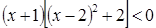 . Решениями неравенства являются все
. Решениями неравенства являются все 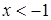 . Аналогично показывают, что решениями неравенства
. Аналогично показывают, что решениями неравенства 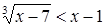 являются все
являются все 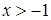 .
.
Следовательно, требуемое утверждение доказано, и исходное уравнение имеет единственный корень 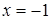 .
.
Ответ. 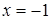 .
.
Тождественные преобразования при решении иррациональных уравнений
При решении иррациональных уравнений и неравенств часто приходится применять тождественные преобразования, связанные с использованием известных формул. К сожалению, такие действия столь же небезопасны, как уже рассмотренное возведение в четную степень, так как иногда приводят к потере или приобретению посторонних решений.
Рассмотрим несколько ситуаций, при которых указанные проблемы возникают.
Пример. Решим уравнение: 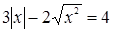 .
.
Решение. При первом же взгляде на это уравнение возникает мысль избавиться от корня с помощью «преобразования» 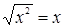 . Однако, так поступать не следует, так как при отрицательных значениях x оказывалось бы, что
. Однако, так поступать не следует, так как при отрицательных значениях x оказывалось бы, что 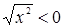 . Здесь целесообразно применить формулу
. Здесь целесообразно применить формулу 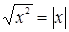 .
.
Применим данную формулу и решим уравнение: 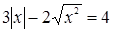
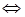
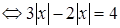
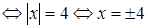 .
.
Ответ. 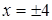 .
.
Рассмотрим «обратное» преобразование.
Пример. Решим уравнение: 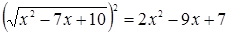 .
.
Решение. В данном случае целесообразно применить формулу: 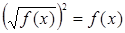 . Исследуем вопрос о безопасности применения данной формулы. Нетрудно видеть, что ее левая и правая части имеют разные области определения и что это равенство верно лишь при условии
. Исследуем вопрос о безопасности применения данной формулы. Нетрудно видеть, что ее левая и правая части имеют разные области определения и что это равенство верно лишь при условии 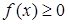 .
.
Поэтому исходное уравнение равносильно системе:
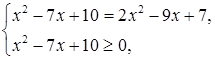
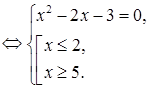
Решим уравнение данной системы, получим корни 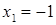 и
и 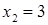 . Второй корень не удовлетворяет совокупности неравенств системы и, следовательно, является посторонним корнем исходного уравнения.
. Второй корень не удовлетворяет совокупности неравенств системы и, следовательно, является посторонним корнем исходного уравнения.
Ответ. 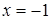 .
.
Следующее опасное преобразование при решении иррациональных уравнений, определяется формулой: 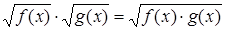 .
.
Если воспользоваться формулой слева направо, область определения исходного уравнения расширяется и можно приобрести посторонние решения. Действительно, в левой части обе функции 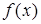 и
и 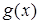 должны быть неотрицательны; а в правой неотрицательным должно быть их произведение.
должны быть неотрицательны; а в правой неотрицательным должно быть их произведение.
Пример. Решим уравнение: 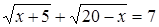 .
.
Решение. Возведем обе части уравнения в квадрат, приведем подобные члены, перенесем слагаемые из одной части равенства в другую и умножим обе части на 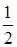 . В результате получим уравнение
. В результате получим уравнение 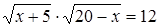 , являющееся следствием исходного уравнения.
, являющееся следствием исходного уравнения.
Снова возведем обе части уравнения в квадрат. Получим уравнение 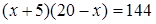 , которое приведем к виду
, которое приведем к виду 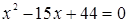 . Полученное уравнение, также являющееся следствием исходного, имеет корни
. Полученное уравнение, также являющееся следствием исходного, имеет корни 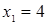 ,
, 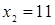 . Оба корня, как показывает проверка, удовлетворяют исходному уравнению.
. Оба корня, как показывает проверка, удовлетворяют исходному уравнению.
Ответ. 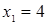 ,
, 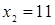 .
.
Замечание. При возведении уравнения в квадрат нередко в уравнении типа 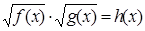 производят перемножение подкоренных выражений, то есть вместо такого уравнения пишут уравнение:
производят перемножение подкоренных выражений, то есть вместо такого уравнения пишут уравнение: 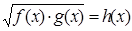 .
.
Такое «склеивание» не приводит к ошибкам, поскольку такое уравнение является следствием уравнения 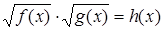 . Следует, однако, иметь в виду, что в общем случае такое перемножение подкоренных выражений дает неравносильные уравнения.
. Следует, однако, иметь в виду, что в общем случае такое перемножение подкоренных выражений дает неравносильные уравнения.
Поэтому в рассмотренном выше примере можно было сначала перенести один из радикалов в правую часть уравнения, то есть уединить один радикал. Тогда в левой части уравнения останется один радикал, и после возведения обеих частей уравнения в квадрат в левой части уравнения получится рациональное выражение.
Рассмотрим пример, где реализуется проблема с использованием формулы: 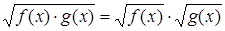 .
.
Пример. Решим уравнение: 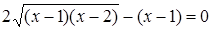 .
.
Решение. Попробуем решить это уравнение разложением на множители:
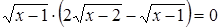 . Заметим, что при этом действии оказалось потерянным решение
. Заметим, что при этом действии оказалось потерянным решение 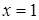 , так как оно подходит к исходному уравнению и уже не подходит к полученному: выражение
, так как оно подходит к исходному уравнению и уже не подходит к полученному: выражение 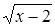 не имеет смысла при
не имеет смысла при 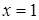 .
.
Поэтому данное уравнение лучше решать обычным возведением в квадрат:
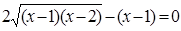
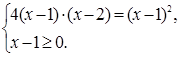
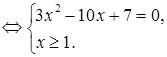
Решим уравнение этой системы, получим корни 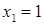 и
и 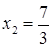 . Оба корня удовлетворяют неравенству исходной системы.
. Оба корня удовлетворяют неравенству исходной системы.
Ответ. 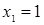 ,
, 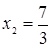 .
.
Таким образом, имеется два пути: или аккуратно возводить уравнение в квадрат, или безошибочно определять, какие решения могли быть потеряны, и проверить, не случилось ли этого на самом деле.
Существует еще более опасное действие – сокращение на общий множитель.
Пример. Решим уравнение: 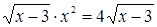 .
.
Неверное рассуждение: Сократим обе части уравнения на 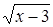 , получим:
, получим: 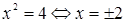 .
.
Совершать такое действие неправомерно, так как во-первых, подходящее решение исходного уравнения 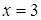 было потеряно; во-вторых, было приобретено два посторонних решения
было потеряно; во-вторых, было приобретено два посторонних решения 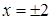 . Таким образом, новое уравнение не имеет ничего общего с исходным.
. Таким образом, новое уравнение не имеет ничего общего с исходным.
Приведем правильное решение.
Решение. Перенесем все члены в левую часть уравнения и разложим ее на множители 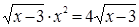
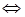
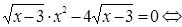
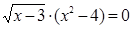 .
.
Уравнение равносильно системе: 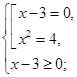 которая имеет единственное решение
которая имеет единственное решение 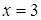 .
.
Ответ. 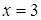 .
.
Иррациональные неравенства
Определение. Иррациональным называютнеравенство, в котором переменная содержится под знаком корня или возведена в дробную степень.
Способ решения иррациональных неравенств состоит в преобразовании их к рациональным неравенствам путем возведения обеих частей неравенства в степень. При этом следует рассматривать только те значения переменной, при которых все входящие в неравенство функции определены, то есть найти область определения неравенства, затем обоснованно осуществлять равносильный переход на всей области определения неравенства или ее частях.
При решении иррациональных неравенств, следует помнить, что при возведении обеих частей неравенства в нечетную степень всегда получается неравенство, равносильное данному неравенству. Если при решении уравнений в результате возведения в четную степень можно получить посторонние корни (что, как правило, легко проверить) и не могли потерять корни, то корни неравенства при бездумном возведении в четную степень могут одновременно и теряться, и приобретаться.
Например, возведя в квадрат:
- верное неравенство 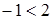 , получим верное неравенство
, получим верное неравенство 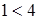 ;
;
- верное неравенство 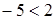 , получим неверное неравенство
, получим неверное неравенство 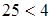 ;
;
- неверное неравенство 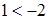 , получим верное неравенство
, получим верное неравенство 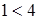 ;
;
- неверное неравенство 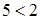 , получим неверное неравенство
, получим неверное неравенство 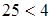 .
.
Таким образом, возможны все комбинации верных и неверных неравенств.
Сформулируем несколько утверждений, которые будем использовать при решении иррациональных неравенств.
Утверждение 1. Если обе части неравенства возвести в четную степень, то получим неравенство, равносильное исходному, в том, и только в том случае, если обе части исходного неравенства неотрицательны.
Утверждение 2. Если обе части неравенства возвести в нечетную степень, то получим неравенство, равносильное исходному.
Утверждение 3. Неравенство вида 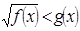 равносильно системе неравенств:
равносильно системе неравенств: 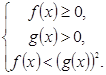
Утверждение 4. Неравенство вида 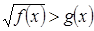 равносильно совокупности двух систем:
равносильно совокупности двух систем: 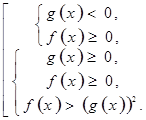
|
|
 2015-07-02
2015-07-02 29026
29026